User:Jules/transformationmatrix
I got some constellation shapes by looking for children activities consisting in Graphing simple constellation.
http://www.spacefoundation.org/sites/default/files/lessonbank/addendums/%5B6-8%5DMapping%20Constellations.pdf
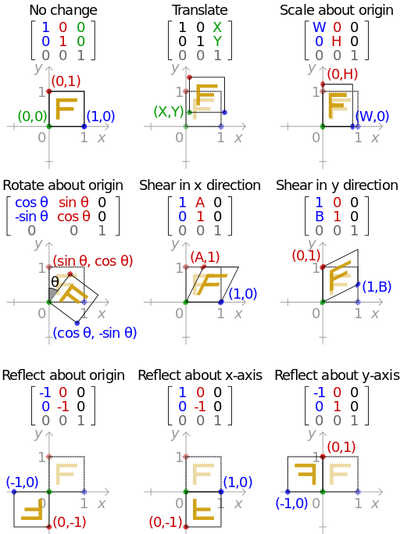
To keep the shape proportionate and enable it to rotate, I had to learn about how to work with a transformation matrix. (luckily enough Ruben teaches me Maths very well)
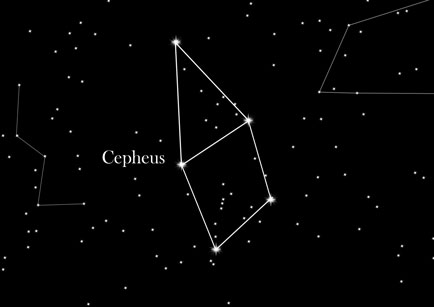
I picked Cepheus to start with an easy one.
These are the coordinates I got :
(2,24); (7,24); (12,27); (7,29); (1,30)
So from that I wanted to calculate the stars position from the first one in the list, becoming the origin.
stars = ([0,0], [5,0], [10,3], [5,5], [-1,6])
So the first thing to do was to find the vector determining the direction.
direction_vector = va - v1
va corresponds to actual coordinates from the database or possible position of starA - starB.
v1 is the same with the proportions instead of actual coordinates from the database.
So far I have this python code to work with:
#Les points de Cepheus: (2,24); (7,24); (12,27); (7,29); (1,30)
#Les points de Cepheus: (0,0); (5,0); (10,3); (5,5); (-1,6)
import numpy as np
# Define a shape
points = ([0,0], [5,0], [10,3], [5,5], [-1,6])
v1 = np.array(points[1])
#v2 = np.array([10,3])
#v3 = np.array([1,1])
#va = np.array([1,0])
# va = starA - starB = [lat,lon] - [lat,lon]
va = np.array([0,0]) - np.array([1,0])
v_dir = va - v1
cosTheta = (np.dot(v1,va) / (np.linalg.norm(v1) * np.linalg.norm(va)))
theta = np.arccos(cosTheta)
sinTheta = np.sin(theta)
scale = np.linalg.norm(va) / np.linalg.norm(v1)
cosTheta = cosTheta * scale
sinTheta = sinTheta * scale
# Rotating Counterclockwise
if v_dir[0] < 0:
transformM = np.array([[cosTheta, -sinTheta],[sinTheta, cosTheta]])
# rotating clockwise
else:
transformM = np.array([[cosTheta, sinTheta],[-sinTheta, cosTheta]])
print transformM
np.dot(transformM, v1)
for point in points:
print np.dot(transformM, np.array(point))