User:Lieven Van Speybroeck/Prototyping/7-Bob Mondriaan

Presenting Bob Mondriaan!
The idea is that the same code generates different 'paintings'. I tried using Inkscape to get colors involved, but somehow, things are not working properly.
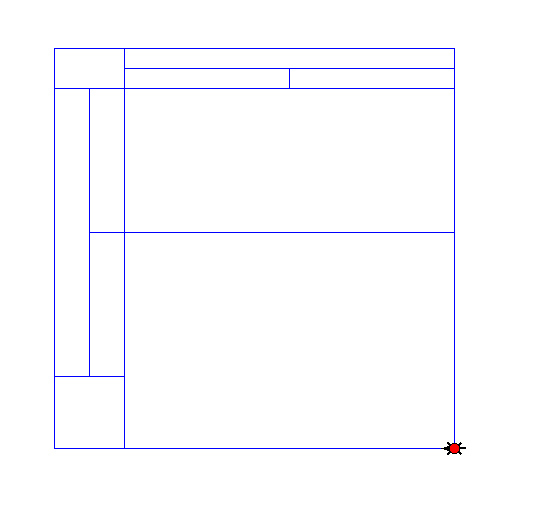
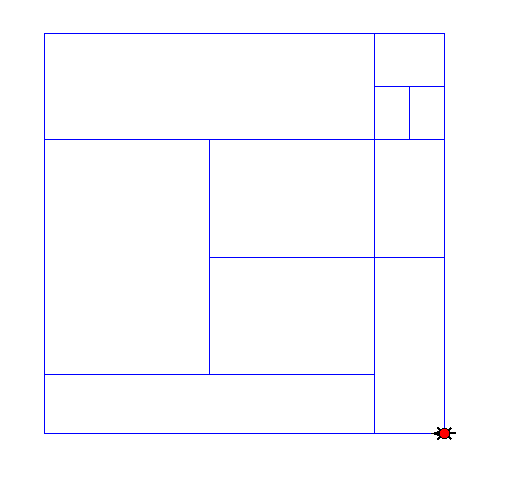
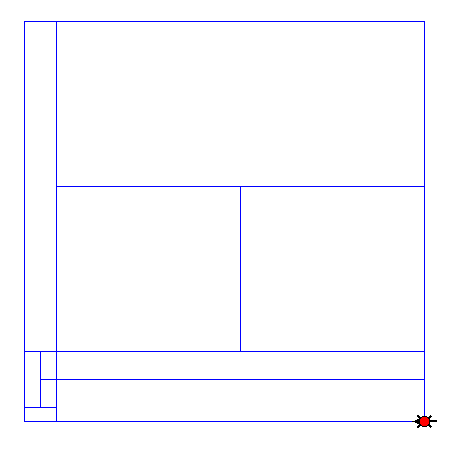
So for now, I can show the TurtleWorld output (colors are quite crucial, I know):

These images consist of full rectangles that could be filled with a random color (obviously white, blue, red or yellow).

The code is a bit of a mess, and I'm still thinking of how I could 'automate' more instead of all the hardcoding:

from TurtleWorld import *
import math
import random

world = TurtleWorld()
bob = Turtle()
bob.delay = 0.01
print bob

def rectangle(t, width, height):
	for i in range(2):
		fd(t, width)
		rt(t)
		fd(t, height)
		rt(t)


def mondriaan(t, scale):
	# omtrek
	rectangle(t, scale, scale)
	
	newWidth = random.randint(3,scale)
	newHeight = random.randint(3,scale)
	
	# rectangle 1
	rectangle(t, newWidth, newHeight)
	fd(t, newWidth)
	
	restWidth = scale - newWidth
	restHeight = scale - newHeight

	# rectangle 2
	rectangle(t, restWidth, newHeight/2)
	rt(t)
	fd(t, newHeight/2)
	lt(t)
	
	# rectangle 3
	for i in range(2):
		rectangle(t, restWidth/2, newHeight/2)
		fd(t, restWidth/2)
	
	rt(t)
	fd(t, newHeight/2)
	

	#rectangle 4
	rectangle(t, restHeight/2.5, restWidth)
	rt(t)
	fd(t, restWidth)
	lt(t)
	
	#rectangle 5
	for i in range(2):
		rectangle(t, restHeight/2.5, newWidth/2)
		fd(t, restHeight/2.5)
	
	rt(t)
	fd(t, newWidth/2)

	#rectangle 6
	rectangle(t, newWidth/2, (restHeight/2.5)*2)

	fd(t, newWidth/2)
	lt(t)
	lt(t)
	
	#rectangle 7
	rectangle(t, newWidth, (restHeight/2.5)*0.5)
	
	pu(t)
	fd(t, scale)
	rt(t)
	fd(t, (restHeight/2.5)*0.5)
	rt(t)
	pd(t)
	
	#rectangle 8
	rectangle(t, restWidth, (restHeight/2.5)*1.5)	


mondriaan(bob, 400)

wait_for_user()

SVG code (not working... but we could have a look at it)

import random
import math

def rectangle(width, height):
	for i in range(2):
		pd()
		fd(width)
		rt(90)
		fd(height)
		rt(90)
		colors = ['255,0.0', '0,255,0', '0,0,255', '255,255,255', '0,0,0']
		color = choice(color)
		styles['fill'] = color
		(pu)

def mondriaan(scale):
	# omtrek
	rectangle(scale, scale)
	
	newWidth = random.randint(3,scale)
	newHeight = random.randint(3,scale)
	
	# rechthoek 1
	rectangle(newWidth, newHeight)
	fd(newWidth)
	
	restWidth = scale - newWidth
	restHeight = scale - newHeight

	# rechthoek 2
	rectangle(restWidth, newHeight/2)
	rt(90)
	fd(newHeight/2)
	lt(90)
	
	# rechthoek 3
	for i in range(2):
		rectangle(restWidth/2, newHeight/2)
		fd(restWidth/2)
	
	rt(90)
	fd(newHeight/2)
	

	#rechthoek 4
	rectangle(restHeight/2.5, restWidth)
	rt(90)
	fd(restWidth)
	lt(90)
	
	#rechthoek 5
	for i in range(2):
		rectangle(restHeight/2.5, newWidth/2)
		fd(restHeight/2.5)
	
	rt(90)
	fd(newWidth/2)

	#rechthoek 6
	rectangle(newWidth/2, (restHeight/2.5)*2)

	fd(newWidth/2)
	lt(90)
	lt(90)
	
	#rechthoek 7
	rectangle(newWidth, (restHeight/2.5)*0.5)
	
	pu()
	fd(scale)
	rt(90)
	fd((restHeight/2.5)*0.5)
	rt(90)
	pd()
	
	#rechthoek 8
	rectangle(restWidth, (restHeight/2.5)*1.5)


mondriaan(400)