Human Computation: Adding Machine: Difference between revisions
m (moved HumanComputation to Human Computation: Adding Machine) |
No edit summary |
||
| (30 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Image:HumanComputation_HumanAddingMachineComputers.png|thumb]] [[Image:HumanComputation_HumanAddingMachineInputs.png|thumb]] | [[Image:HumanComputation_HumanAddingMachineComputers.png|thumb]] [[Image:HumanComputation_HumanAddingMachineInputs.png|thumb]] | ||
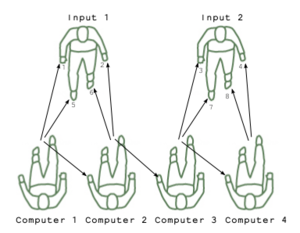
A procedure to be performed by 6 people (plus, | A procedure to be performed by 6 people (plus, 1 operator and 1 clock). | ||
Implements a 4-bit adder, capable of adding a series of numbers (from 0 - 15). The final result may be as large as 31 (as long as no intermediate sum totals more than 15 due to the 4-bit limitation of the input / latch). | |||
Image credit: Human figure drawings by [http://www.speculoos.com/ Pierre Huyghebaert], released under a [[Free Art License]] | |||
= Rules for performing an "Human Adding Machine" = | = Rules for performing an "Human Adding Machine" = | ||
| Line 24: | Line 24: | ||
== Computation == | == Computation == | ||
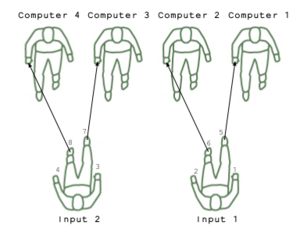
You | You observe 3 "signals": one side (hand and foot) of the "encoder" seated in front of you, as well as the left (near) hand of the person seated to your right (if there is someone). You raise your hands to reflect the number of signals (raised hands or foot) you observe according to the following: | ||
{| class="wikitable" | |||
|0||Neither hand raised (both hands down) | |||
|- | |||
|1||Raise your right hand only | |||
|- | |||
|2||Raise your left hand only | |||
|- | |||
|3||Raise both your left and right hands | |||
|} | |||
=== Computer 1 === | |||
("Most significant bit")<br /> | |||
You observe the left side (the right hand and foot) of Encoder 1 (seated in front of you) and the left hand of Computer 2 (seated to your right). | |||
=== Computer 2 === | |||
You observe the right side (the left hand and foot) of Encoder 1 (seated in front of you) and the left hand of Computer 3 (seated to your right). | |||
=== Computer 3 === | |||
You observe the left side (the right hand and foot) of Encoder 2 (seated in front of you) and the left hand of Computer 4 (seated to your right). | |||
=== Computer 4 === | |||
("Least significant bit")<br /> | |||
You observe the right side (the left hand and foot) of Encoder 2 (seated in front of you). You only observe a maximum of 2 signals. | |||
At this point, the current result of the addition may be observed based on the hands of the computers ([[#Decoding]]). If an additional number should be added, proceed to the [[#Latch]]. | At this point, the current result of the addition may be observed based on the hands of the computers ([[#Decoding]]). If an additional number should be added, proceed to the [[#Latch]]. | ||
| Line 63: | Line 80: | ||
</source> | </source> | ||
== Downloads == | |||
*[[File:HumanComputation_HumanAddingMachine.pdf]] | |||
== Performances == | |||
{{video|webm=http://pzwart1.wdka.hro.nl/~mmurtaugh/video/hc2012_binary.160p.webm}} {{video|webm=http://pzwiki.wdka.nl/mw-mediadesign/images/8/8f/Hc2012_adder.160p.webm}} | |||
[[File:Humancomputer2018.jpg|thumb|performing 4 bit addition in 2018]] | |||
{{video|mp4=http://pzwart1.wdka.hro.nl/~mmurtaugh/video/HumanComputation-2012-09-17.m4v|Human computing in 2012}} | |||
{{video|mp4=http://pzwart1.wdka.hro.nl/~mmurtaugh/video/HumanComputation2018.mp4|Human computing in 2018|style=width:640px;}} | |||
* [[File:HumanComputation-2012-09-17.webm]] | |||
* [[File:Hc2012 adder.160p.webm]] | |||
| Line 68: | Line 101: | ||
[[Category:Cookbook]] | [[Category:Cookbook]] | ||
== Links == | |||
== | * "Did increases in the power of mathematics lead the development of calculators? Was it the other way round?" ... http://meta-studies.net/pmwiki/pmwiki.php?n=Site.Introduction | ||
* | |||
Latest revision as of 10:56, 27 June 2023
A procedure to be performed by 6 people (plus, 1 operator and 1 clock).
Implements a 4-bit adder, capable of adding a series of numbers (from 0 - 15). The final result may be as large as 31 (as long as no intermediate sum totals more than 15 due to the 4-bit limitation of the input / latch).
Image credit: Human figure drawings by Pierre Huyghebaert, released under a Free Art License
Rules for performing an "Human Adding Machine"
(for 6 people)
Input
To be performed by the Operator. (If no operator is present, the role can be performed by one of the computers).
The input number is written on a card.
If the number is 8 or larger: subtract 8 from the number and write the new number (crossing out the old) and ask Input 1 to raise their right hand. If the (new) number is 4 or larger: subtract 4 from the number and write the new number (crossing out the old) and ask Input 1 to raise their left hand.
If the (new) number is 2 or larger: subtract 2 from the number and write the new number (crossing out the old) and ask Input 2 to raise their right hand. If the remaining number is 1: ask Input 2 to raise their left hand.
NB: Input can also be performed by having the operator stand behind the inputs and then tap the respective shoulder of the input to indicate that a hand should be raised.
Computation
You observe 3 "signals": one side (hand and foot) of the "encoder" seated in front of you, as well as the left (near) hand of the person seated to your right (if there is someone). You raise your hands to reflect the number of signals (raised hands or foot) you observe according to the following:
| 0 | Neither hand raised (both hands down) |
| 1 | Raise your right hand only |
| 2 | Raise your left hand only |
| 3 | Raise both your left and right hands |
Computer 1
("Most significant bit")
You observe the left side (the right hand and foot) of Encoder 1 (seated in front of you) and the left hand of Computer 2 (seated to your right).
Computer 2
You observe the right side (the left hand and foot) of Encoder 1 (seated in front of you) and the left hand of Computer 3 (seated to your right).
Computer 3
You observe the left side (the right hand and foot) of Encoder 2 (seated in front of you) and the left hand of Computer 4 (seated to your right).
Computer 4
("Least significant bit")
You observe the right side (the left hand and foot) of Encoder 2 (seated in front of you). You only observe a maximum of 2 signals.
At this point, the current result of the addition may be observed based on the hands of the computers (#Decoding). If an additional number should be added, proceed to the #Latch.
Latch
Rules for the Latch, performed by the Inputs:
Raise or lower your feet to mirror the right hands of the two "computers" seated in front of you (left foot for left computer, right foot for right computer, extend your foot if the hand is raised, lower your foot if not).
At this point all hands may be lowered, and a new number added via #Input
Decoding
Add the scores according to the following:
Computer 1's left hand:
16 points
Computer 1's right hand:
8 points
Computer 2's right hand:
4 points
Computer 3's right hand:
2 points
Computer 4's right hand:
1 point
Downloads
Performances
Links
- "Did increases in the power of mathematics lead the development of calculators? Was it the other way round?" ... http://meta-studies.net/pmwiki/pmwiki.php?n=Site.Introduction