User:Simon/Special Issue 8/summary first half trim
Mapping network topologies
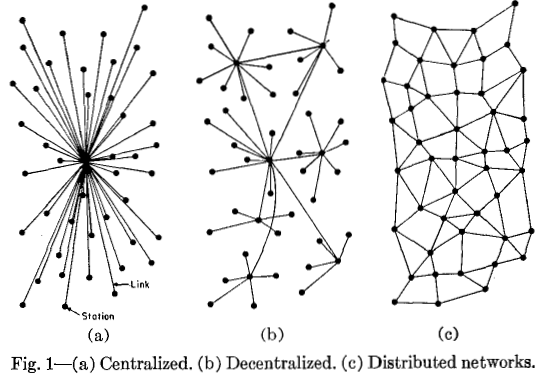
Paul Baran diagrams
We started with a reading of a text on centralised, decentralised, and distributed networks that included a diagram made by Paul Baran for the RAND corporation. This diagram displays classic ways to visualise these networks.
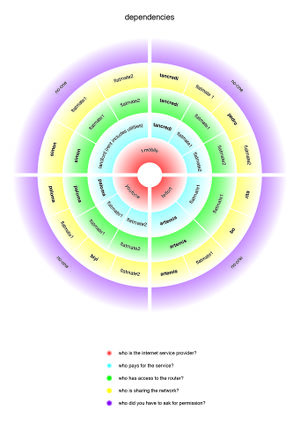
Dependency mapping task
As part of the Infrastuctour, when we set up our homeservers, I worked with Artemis to create a visualisation of the dependencies involved setting them up.
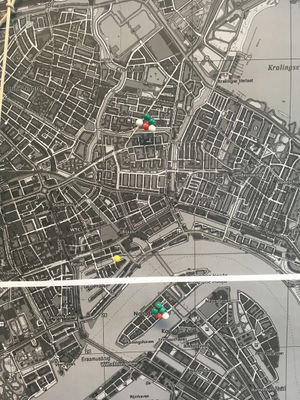
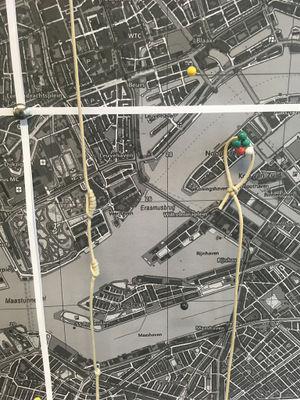
Physical map in XPUB studio
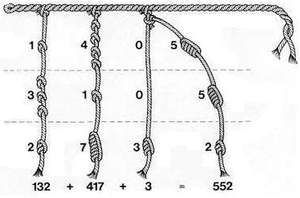
I made a map of the location of homeservers and routers, including the other (non-XPUB) network users as well as situations where it was not possible for XPUB students to connect their server to their home router, and so had to depend on others. Manetta introduced me to Inca Quipu, a way that the Inca recorded numbers by tying knots in strings.
I connected a piece of string I'd tied knots in to represent my external IP address for my home server, as a way to visualise the idea of connecting and also the route that a client follows when connecting to my website, which is in reverse from the way I would display my IP.
Collection of texts
I've begun collecting relevant texts to my research and creating html pages to store them on my website. This has been a useful way to develop my web design knowledge and skills as well as provide theoretical basis for the research I'm undertaking into network topologies.
Tung-Hui Hu: Truckstops on the Information Superhighway
http://b-e-e-t.r-o-o-t.net/pages/truckstops_on_the_information_superhighway.html
Paul Rand: Cybernetic Guerilla Warfare (Radical Software 1.3)
http://b-e-e-t.r-o-o-t.net/pages/cybernetic_guerilla_warfare.html
R. Buckminster Fuller: Software (Radical Software 1.1)
http://b-e-e-t.r-o-o-t.net/pages/buckminster_fuller_software.html
These texts introduced me to alternative models for mapping topologies such as "klein worms", referred to in both Hui (2015) and Rand's (1970) texts. Klien worms are based on the klein bottle, which falls into the category of "topologically impossible" objects (such as moebius strips etc.).
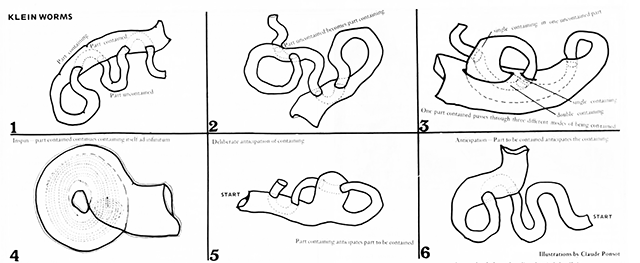
Paranodal activity
The concept of paranode (as suggested in Constant's Feminist Server Manifesto, and further explored by Zach Blas) was intriguing, and I resolved to keep this in mind when mapping network topologies. I see the paranode as both a disruptive concept (the thing that isn't there?), also not related to physical devices (established as nodes, but instead on social and conceptual relations between people and the world). I took initial references from the SI concept of the derive as a way to rethink autonomy in public space.
On further reading I found this article:
http://www.christydena.com/2007/08/new-network-theory-the-tyranny-of-nodes/
The author defines the paranodal in this way: the space between nodes; the space that is not dead, but very much alive.
The author also uses Ranciere's terminology, saying: the paranodal is "the part of those who have no part", where we experience what it is to be outside of the network while still being related to it.
Maps and autonomy
I began recording some of my thoughts around the concept of contingent autonomy and how it relates to mapping. These refer to the map/territory problem, which sees a 1:1 map as redundant (and therefore useless) and also Hakim Bey's Temporary Autonomous Zone concept (introduced to me by Tancre), where the 1:1 map is the only possible way for someone to have autonomy.
https://pad.xpub.nl/p/map_thoughts
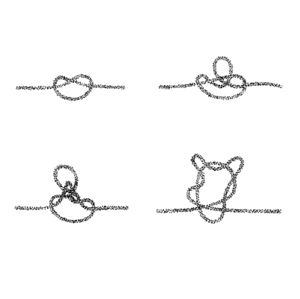
Topology and Graphology
Early references explored knot theory, a study in mathematics which takes knots as topological forms. I found these interesting as alternative models of topology to the one presented by Baran; also as Roel pointed out, the etymology of the word "node" comes from the word for "knot".
Michael introduced me to Jacqueline de Jong's Situationist Times, which I found interesting (particularly Issue 3: Topology).
My research led me to discover the famous Seven Bridges of Königsberg (now Kaliningrad, Russia) problem, which prefigured topology and laid foundations for graphology (a graphic mapping of topologies). The problem asked how to devise a walk across these bridges, crossing each one only once. This was answered as impossible by Euler, who also demonstrated how the physical landscape could easily be abstracted into a graph.
Seven Bridges of Konigsberg
I also began to draw examples of network topologies based on the form of knots that I had explored with making of the physical map. I was interested in how the knots could represent physical, linear movements of data, but when in silhouette, resembled representations of distributed networks.
Modularity
I began to make small sculptural models of theoretical network topologies out of polymer clay, which resembled mathematical knots.

These developed into a model which incorporated a wooden board with regular holes drilled in it, kind of a static interface that these loops and knots could be inserted into, in a similar way to a modular synthesiser. This was partly inspired by a session in which artist Aditya Mandayam demonstrated use of the Plumbutter2, a modular synthesiser that comes with a manifesto and also represents a "map of Baltimore".