User:Simon/Special Issue 8/The Network we (de)Served part 3

The Network we (de)Served, Part 3: From Networks to Knotworks publication

Early on in my research into network topologies I discovered the klein form, a "non-orientable surface".

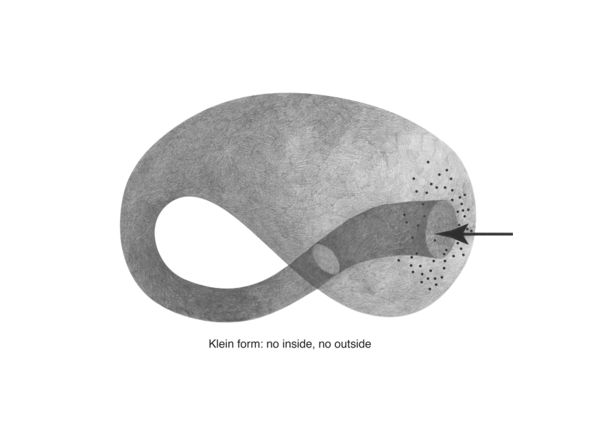
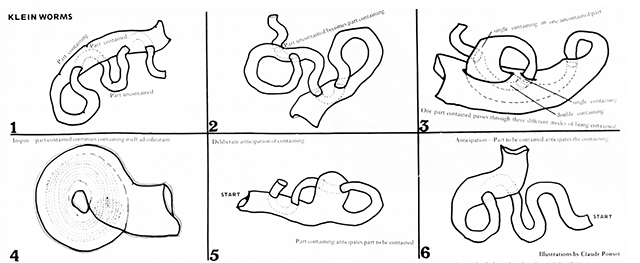
Klein forms are the basis for the "topologically impossible" klein worms. I first came across these in the first half of the trimester as illustrations in the article "Cybernetic Guerilla Warfare" from the media art newsletter Radical Software:

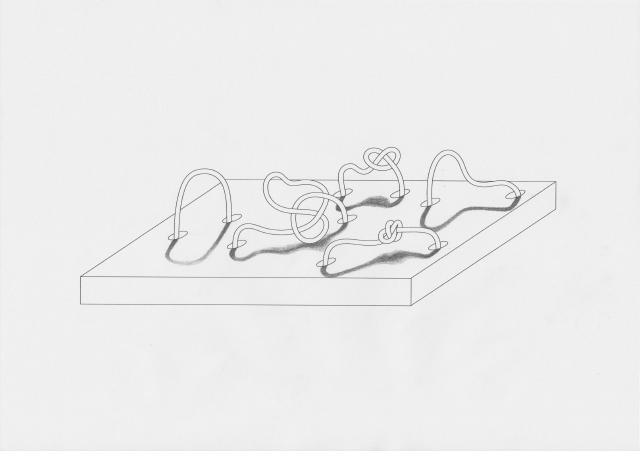
The networked methodology I was working with included shifting between different outcomes and actions. This made me think of also a shift between two-dimensional and three-dimensional forms, and thinking about how these could be "unfolded":

The knotboard I had made in the first half of the trimester proved a useful tool for thinking with my hands. I noticed that as a physical object, it was different from my drawings as it immediately had depth, and form, and as a result was affected by light, particularly shadows:

When configured in different ways (especially as a three-dimensional form) the knotboard took on a different presence. I made drawings from this, incorporating light and shadow as well as alternative ways of imagining the three-dimensional space the knotted links occupied:

Research into knot theory (a field of mathematics which studies the topology of knots) led me to discovering mathematical knots, which are different from the usual idea of a knot. I had previously explored knots as ways to record numbers (a notable reference being Quipu from ancient Andean cultures):

Mathematical knots are different, in that they are based on the embedding of a circle into three-dimensional Euclidean geometry R3. As such, they resemble closed loops. The first of these is the "unknot":

Visualisation is a powerful tool when communicating alternative ways of thinking and "seeing" things. Through visualisation, I found another way of thinking about nodes and links. I made "Knotwork" drawings of knots with eight crossings, each representing a node in our homebrewed network. The crossings could be seen as redistribution points (as in the classic definition of a node), or perhaps an overlapping area of linkage. In respect to thinking about nodes as knots, I found that when the knot is unraveled, the nodes and the links are the same thing.

The Network we (de)Served Publication

My research was published in the form of both web- and printed zines.

Web zine

The web zine is available at: https://issue.xpub.nl/08/Research/b-e-e-t.r-o-o-t.net/

An alternate on-page layout is also available at: http://beetroot.simonbrowne.biz

1. An A2 cover (folded down to A4) with drawings made by a pen plotter of my GPS walks. 2. My research pages. These are unbound, with a rotating orientation of text an image. The idea was to allow the reader to reorder pages and create their own pagination. 3. A collection of texts I have published online that influenced my thinking during the project. This is bound, and printed on blue paper to differentiate it from the rest of the zine.