User:Simon/Special Issue 8/The Network we (de)Served part 2

The Network we (de)Served, Part 2: Visualising network topologies

topology and graphology

Early references explored knot theory, a study in mathematics which takes knots as topological forms. I found these interesting as alternative models of topology to the one presented by Baran; also as Roel pointed out, the etymology of the word "node" comes from the word for "knot".

Michael introduced me to Jacqueline de Jong's Situationist Times, which I found interesting (particularly Issue 3: Topology).

My research led me to discover the famous Seven Bridges of Königsberg (now Kaliningrad, Russia) problem, which prefigured topology and laid foundations for graphology (a graphic mapping of topologies). The problem asked how to devise a walk across these bridges, crossing each one only once. This was answered as impossible by Euler, who also demonstrated how the physical landscape could easily be abstracted into a graph.
Seven Bridges of Konigsberg

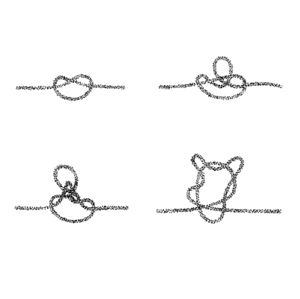
I also began to draw examples of network topologies based on the form of knots that I had explored with making of the physical map. I was interested in how the knots could represent physical, linear movements of data, but when in silhouette, resembled representations of distributed networks.

modularity

I began to make small sculptural models of theoretical network topologies out of polymer clay, which resembled mathematical knots.

These developed into a model which incorporated a wooden board with regular holes drilled in it, kind of a static interface that these loops and knots could be inserted into, in a similar way to a modular synthesiser. This was partly inspired by a session in which artist Aditya Mandayam demonstrated use of the Plumbutter2, a modular synthesiser that comes with a manifesto and also represents a "map of Baltimore".

network of possibilities

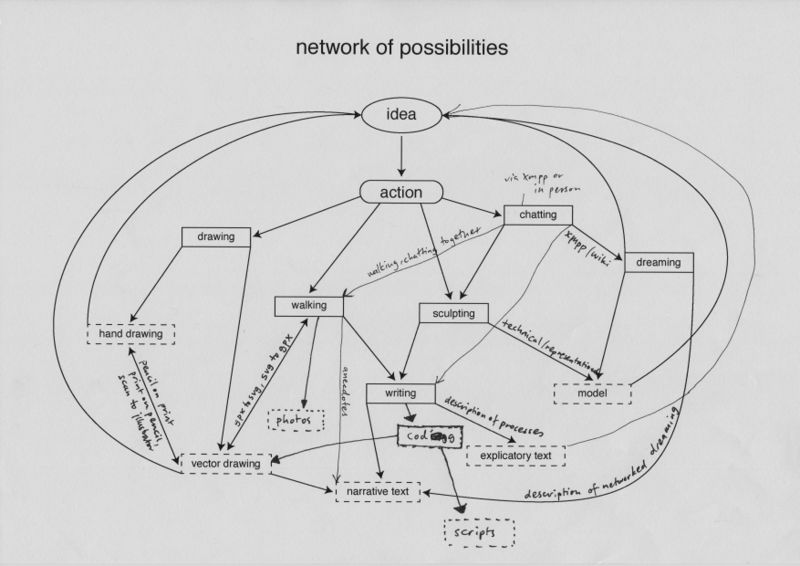
I began the second half of the trimester by determining a networked methodology for producing outcomes. The aim was to develop a heuristic; a technique which would help me understand networks better through a looped system of ideas, actions and outcomes.

gps walking

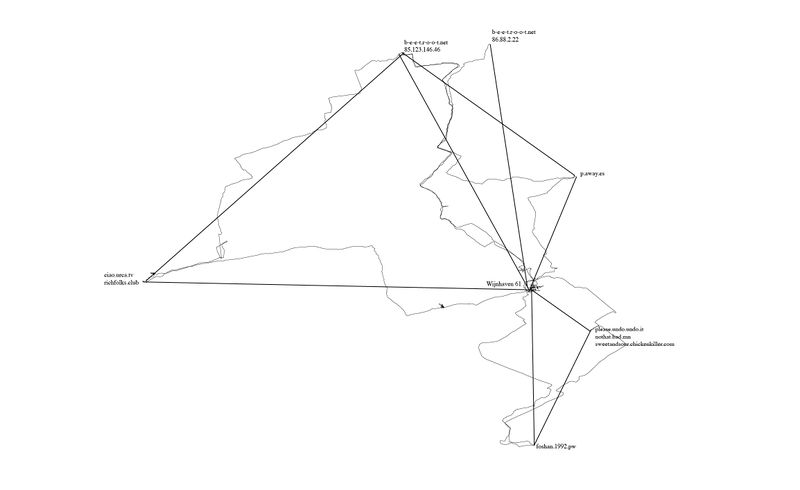
One of the actions I included in my network of possibilities was to begin walking between different points in our network (our homeservers, and also the PZI building where we gathered to have classes and work on Special Issue 08).



I used a hiking app called "Trails", which would record my walk over GPS, from which I could export the .gpx file generated after walking, and then load it into a program for geospatial information called QGIS. An interesting feature of this software is in how it represents the line created by walking - you can upload it as trackpoints (snapshots of your location determined by satellite trilateration), and also as straight lines between the trackpoints. I started to realise how abstraction was a large part of mapping, which reminded me of the map/territory problem.

I began to make drawings, which, by being devoid of text that would explain them, could act as illustrations of how this map was being made:

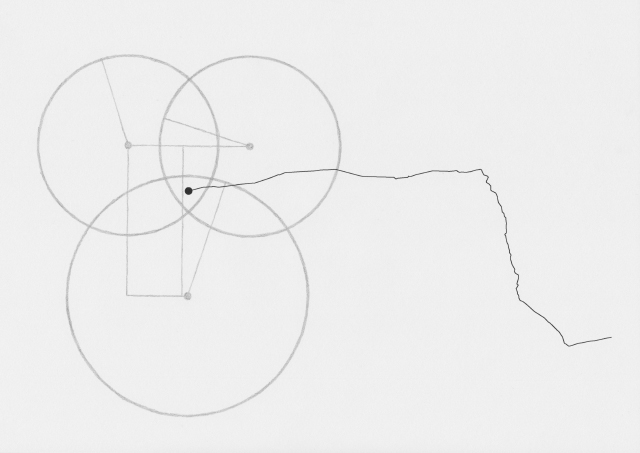
During each walk I would take photos and write notes on thoughts that came up. I began noticing other networks around me.

Flight paths that produced contrails (or chemtrails):

Public transport networks:

Bicycle networks:

Social networks:

Each walk became an act of drawing (using GPS) and also a meditation.

networked research

I also began to write down my thoughts on various topics that came up, compiling a list of the terms I was beginning to define through my research in relation to a mappable experience of the network.

https://pad.xpub.nl/p/networked_research

As I wanted a fairly horizontal structure to my research, I decided to base the content for each page of my website on a walk.

drawing visualisations

Drawing (by hand and using vectors) became a large part of the outcomes I produced as part of my research. The drawings often shifted between "hand-drawn" and "computer-drawn", for example, I would use a .svg file made from one of my GPS walks in a vector graphics program, then print it and hand-draw with pencil over the top.

Abstraction became a key interest, and I started to think more about how these different ways of visualising all employed some level of abstraction in order to communicate. This brought me back to the typical idea of displaying network topology, as nodes and straight lines:

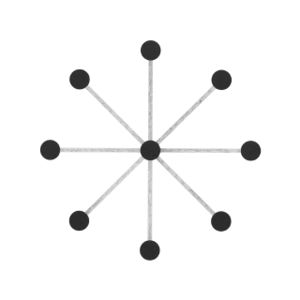
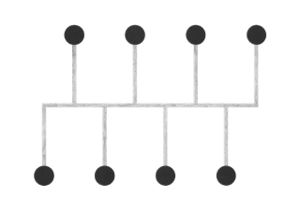
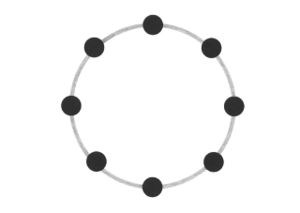
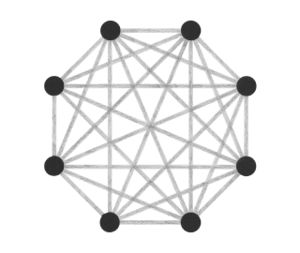
The drawings I made while GPS walking employed straight lines between trackpoints. However, this was just an abstraction - there are no straight lines in reality. In fact, the more accurately I would be able to map the network, the less useful it would be as a readily comprehensible visualisation. I also noticed that at points the GPS signal had become confused or obscured - this happened when I went into buildings (such as a cafe to buy a coffee) or when the signal might have been obscured by tall buildings around me. This produced knots, which I saw as analogous to nodes.

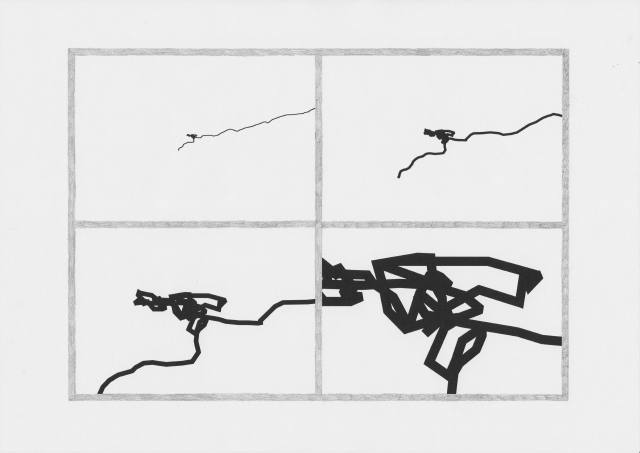
When I imported the lines I made by GPS walking into .svg format, I experimented with unraveling some of these knots, and then drew this process.