User:Laurier Rochon/prototyping/l-systems
L-Systems
An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms. L-systems can also be used to generate self-similar fractals such as iterated function systems. L-systems were introduced and developed in 1968 by the Hungarian theoretical biologist and botanist from the University of Utrecht, Aristid Lindenmayer (1925–1989).
From WikiPlagiat
turtle VS TurtleWorld
Discovery of the day : TURTLE! (not TurtleWorld, the library)
It actually appears that Python has built-in turtle graphics, meaning that we can bypass BOB (being in the 'swampy folder' etc., and just use a 'pointer' triangle, with much clearer methods. This is the page for it. It's well documented - for example, you can use 'setcoords(x,y)' to set the pointer at the right spot. The method 'getheading' is also tremendously useful in knowing what angle bob is oriented towards. One big problem with turtle vs turtle world : it's slowwwwwwwwwwwwww. Max speed is '10', which equates to about '1' in Turtle World terms.
Going green with recursive algorithms
Takes about 20-30 minutes to generate at MAX speed (with TurtleWorld library. About 10X with native turtle lib)
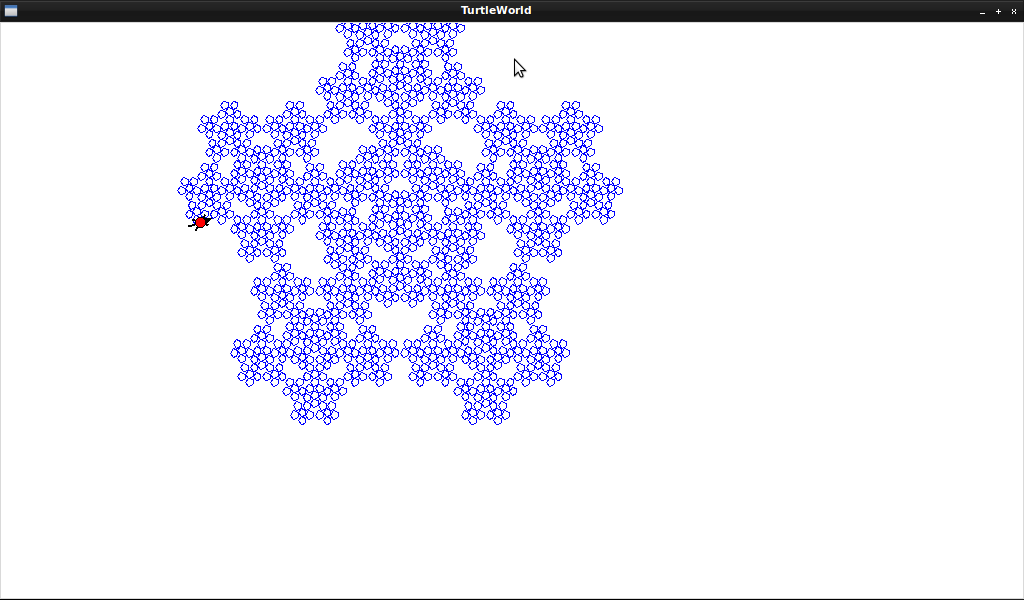
Rules:
- X -> F-[[X]+X]+F[+FX]-X
- F -> FF
Interpretation:
- Start symbol = X
- F = forward 2
- + = right 25
- - = left 25
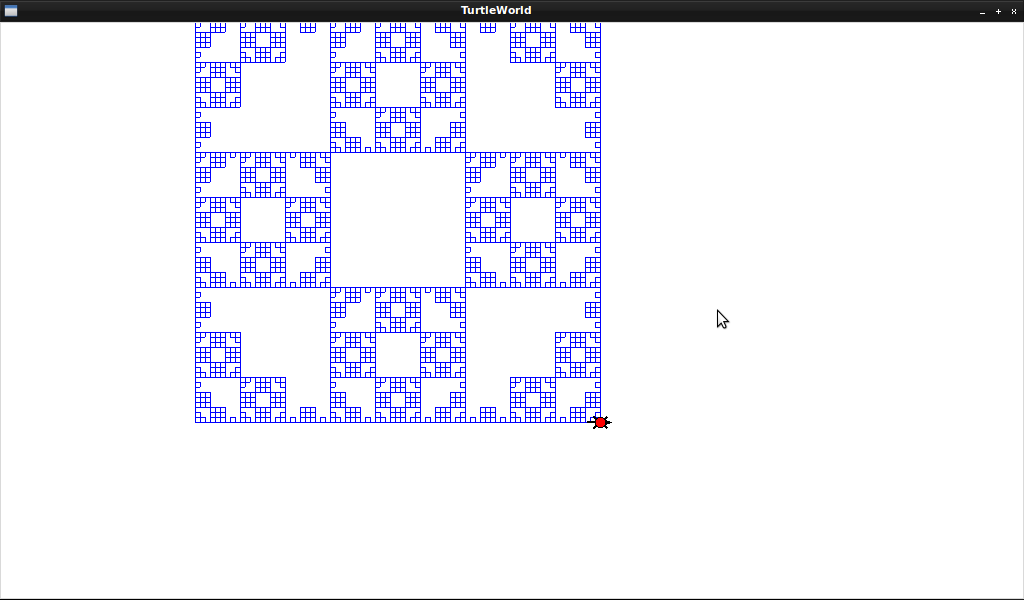
Rule:
- F -> FF-[-F+F+F]+[+F-F-F]
Interpretation:
- Start symbol = F
- F = forward 5
- + = right 25
- - = left 25
(the tree rules I got here.)
Using basic transformation rules such as :
- Axiom: F-F-F-F
- Rule : F -> FF-F-F-F-FF
- Angle: 90
- Steps: 4
What the symbols mean
- F is forward by X pixels
- + is turn Y degrees
- - is turn -Y degrees
- [ is record the current state
- ] restore the matching last ] state
Will yield something like :
Other set of rules...
Soft (Python)
(with TurtleWorld)
from TurtleWorld import *
world = TurtleWorld()
bob = Turtle()
#make it FAST!
bob.delay = 0.0001
#draw upwards, plz
lt(bob,90)
#gimme some room...we'll fullscreen the window
bob.x=200
bob.y=-300
#starting axiom
n = 'X'
#replacement rules
s1 = 'X'
s2 = 'F-[[X]+X]+F[+FX]-X'
s3 = 'F'
s4 = 'FF'
#number of steps
steps = 7
for i in range(steps):
#apply the rules, do the replacements
n = n.replace(s1,s2)
n = n.replace(s3,s4)
#angle to turn
a = 25
#declare my arrays
xx = []
yy = []
angle = []
#go through all characters of my string
for i in n:
#go forward
if i == 'F':
bob.fd(1)
#turn left
if i == '+':
bob.lt(a)
#turn right
if i == '-':
bob.rt(a)
#record current state
if i=='[':
xx.append(bob.get_x())
yy.append(bob.get_y())
angle.append(bob.get_heading())
#restore last state...
if i==']':
#we're gonna move around, put the pen up
bob.pu()
#change x and y
bob.x = xx[len(xx)-1]
bob.y = yy[len(yy)-1]
#cancel whatever angle you're in
bob.rt(bob.get_heading())
#turn to new angle
bob.heading = angle[len(angle)-1]
#pop the x,y and angle off their stacks
xx.pop()
yy.pop()
angle.pop()
#ready to draw again...
bob.pd()
wait_for_user()