User:Thijshijsijsjss/Pen Plotting Panache/Plotillism

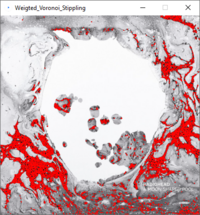
Stippling is a drawing technique by which details are captured by placing points in varying densities and is frequently used in the impressionistic pointillism. This page describes a workflow to convert a digital image to a pointillism version that can be pen plotted.

• Find the code on GitHub

Steps of Weighted Voronoi Stippling visualized (please, enjoy the typo)

Stochastically chosen seed points

Paths of seed points during iterative relaxation

Relaxed seed points after 50 iterations

Relaxed seed points, no background

Relaxation visualized

Pen plotted pointillism plot of Radiohead's A Moon Shaped Pool (mirrored, 400x400px, 20000 points, 50 iterations, 150 threshold)

Technique

(bit of a placeholder, will update later)

1. Randomly place N seed points on your canvas
2. Create the Delaunay diagram for these seed points: the unique triangulation such that the no triangles circumcircle contains any points)
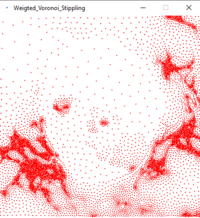
3. Create the Voronoi diagram for these seed points: polygons that represent the areas that contain all coordinates that share the seed point they're closest to. This is the dual graph of the Delaunay diagram (i.e. the vertices in the Voronoi diagram are the centers of the Delaunay circumcircles).
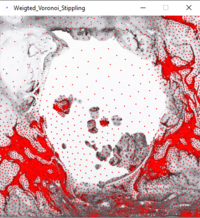
4. Apply Lloyd's Algorithm (Voronoi iteration) by iteratively moving the seed points to the centers of the Voronoi polygons. This can be approximated by the average of the polygon vertices, or better yet be calculated (see Paul Burke's reference).
5. Use these relaxed points for 'pointillism'

Note: for our purposes, we don't simply want to relax all points. This would ultimately lead to a uniform distribution. Instead, we want to base the relaxation on the brightness values of the image we feed in.

References

• Paper introducing Weighted Voronoi Stippling
• Coding Train tutorial and reference code (p5.js using D3 library)
• Wikipedia: Voronoi diagram (basis for relaxation)
• Wikipedia: Delaunay triangulation (dual graph to Voronoi diagram that might be used for optimized pixel-coloring)
• Lloyd's Algorithm (Voronoi iteration) (way of iterative relaxation of seed points)
• Calculating the center of a polygon Paul Burke's reference (not used, this script is using pixel information)