User:Ssstephen/rule-110
Rule 110
Play the universal game
Click anywhere to change a pixel. This is a p5.js version of the cellular automata often referred to as Rule 110. Each cell (black or white square) is generated by simple rules from the three squares above it.
Universality in Elementary Cellular Automata, Matthew Cook
This game has been proven turing complete by Matthew Cook in Universality in Elementary Cellular Automata. In particular a universal computer can be built when using the repeating background pattern 11101100100000. On this background variations can be make to programme "gliders" in a cyclic tag system, which is itself capable of universal computation.
-
-
-
-
-
-
-
-
Because a system is universal, some of its properties are undecidable (will it become periodic, will a particular sequence occur)
Because Turing machines are universal, if a compiler exists that can compile any data and program from a turing machine to another computer, then that computer is also universal
Tag systems are universal ACDABBE --> DABBECCDD
Cyclic tag systems can only have a two letter alphabet {Y,N}, but they can emulate tag systems so are also universal.
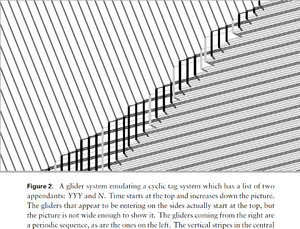
A glider system (see image) is a system of moving particles called gliders. In the image you can see diagonal lines which interact with vertical lines (the tape head or data) in the centre, emulating a cyclic tag system. The glider system is running an emulation of the cyclic tag system, which is running an emulation of the tag system. In a way this looks like a vector system to me, of interacting vectors rather than flipping bits.
Lastly you run an emulation of the glider system inside rule 110.
-
Fabric version of this could be really interesting. If you got a round loom with 14n pins (a flat loom maybe would be more flexible, to decide different sizes), you could knit a hat or sock program. https://www.youtube.com/watch?v=gOTIAmg0Iow Or does it need to be woven? No idea.
The piece should be a ring so the ends more obviously loop back on themselves. Re: slow computing, computation as labour, This Work of Body / This Body of Work, Meghan Clarke https://www.designacademy.nl/p/study-at-dae/graduation-show/graduation-projects/meghan-clarke Talk to Daniela about double sided knitting, re binary knitting and ternary knitting. So the knitting is the computation; knit the first line of the program then knit further to get the output. A little similar to a quipu, although probably a less efficient system. Are quipus universal?
What can you compute on rule 110 (apart from everything)? Can you write a hello world script on a rule 110 computer? Can you add 2+2? https://www.youtube.com/watch?v=QKnSRw_X2w4
First attempts here at coding in the p5.js version of 110 with a few A gliders of increasing widths. Even experimenting on the javascript version of this is so slow, doing this in playing cards or knitting would be incredibly slow. But if it's a statement about computational labour the slowness reveals that.
Stopped at page 13 for now.
Playing this with a deck of cards
- Players are given a large number of cards which are black on one side and white on the other. Players should be in a circle.
- In the first hand everyone plays one card with either side face up, chosen by any method (no rules for this hand! see below for turing complete version of the game).
- Everyone plays a new card based on the last hand's cards (in particular their own and the player on each side of them).
- If you and your neighbours all played the same colour last round, you should play white.
- If the person to your left played black but you and the person to your right played white, you should play white.
- In all other cases, you should play black.
- Keep playing hands until you halt!
Turing complete variation
If you would like this round to be Turing complete you will need 14n players. The simplest place to start is to play the first round as follows:
- player one: white
- player two: white
- player three: white
- player four: black
- player five: white
- player six: white
- player seven: black
- player eight: black
- player nine: white
- player ten: black
- player eleven: black
- player twelve: black
- player thirteen: black
- player fourteen: black
Then proceed by the usual rules. Programs can be written by making variations on the starting hand.
Memoryless version
Each player gets one card and flips it too black or white according to the usual rules. This requires much less cards! An alternative form of memory could be used like time lapse photography.
digital memoryless version
Possibly in a circle