On object

From the discussion on our previous class, I was triggered by the concept of difference when defining an object. This idea that I found more explicitly in Gregory Bateson's text "Form, substance and difference", difference being "that sort of "thing" that gets onto the map from the territory."

More relevant to me seems the idea of movement as the premise for an existing object (for existing I mean both tangible/intangible): "There are differences between the chalk and the rest of the universe, between the chalk and the sun or the moon. And within the piece of chalk, there is for every molecule an infinite number of differences between its location and the locations in which it might have been. Of this infinitude, we select a very limited number, which become information. In fact, what we mean by information—the elementary unit of information—is a difference which makes a difference, and it is able to make a difference because the neural pathways along which it travels and is continually transformed are themselves provided with energy. The pathways are ready to be triggered. We may even say that the question is already implicit in them."

I believe when reading Heidegger the moment object encounters the subject, when it becomes "distanceless" (also the idea of movement implied) was the most striking to me.

ob = against jakere = to throw something so, objection is literally: i throw something towards you .

Body, the physical self. the performer.

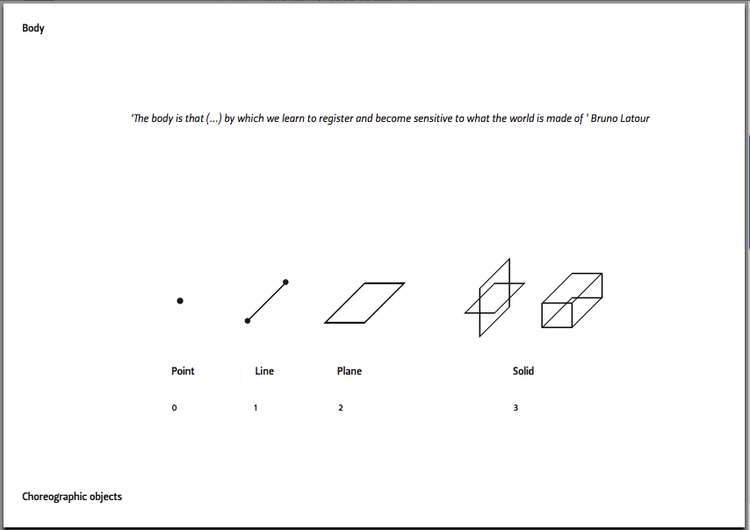
Choreographic Object, following W.Kandinsky reflection on the basic structure of his painting composition, I found interesting to consider using this same representation method as means for writing movement. Language as structure, methodology. This elements allow multiple forms of representation, being graphic, linguistic, geometrical; relying on imagery, sound, and so on. Either ways, meaning is created. I am interested in choreographic objects as existing in themselves as notation systems, and as in its performative state.

0 - Point 1 - Line 2 - Plane 3 - Solid

Dimensions - Symbols

Point : The geometric point is an invisible thing. Therefore, it must be defined as an in- corporeal thing. Considered in terms of substance, it equals zero. Hidden in this zero, however, are various attributes which are “human” in nature. We think of this zero—the geometric point—in relation to the greatest possi- ble brevity, i.e., to the highest degree of restraint which, nevertheless, speaks. Thus we look upon the geometric point as the ultimate and most singular union of silence and speech. The geometric point has, therefore, been given its material form, in the first in- stance, in writing. It belongs to language and signifies silence.

Line: The geometric line is an invisible thing. It is the track made by the moving point; that is, its product. It is created by movement—specifically through the destruction of the intense self-contained repose of the point. Here, the leap out of the static into the dynamic occurs.

Plane: The term “Basic Plane” is understood to mean the material plane which is called upon to receive the content of the work of art. Dematerialized Plane. The elements lying firmly (materially) on a solid, more or less hard and, to the eye, tangible BP and, in contrast, the elements “floating” without material weight in an indefinable (immaterial) space are of fundamentally different appearance, and stand in antithesis to each other.

Movement is indicated as “the transition from one point to the next”, that is as one “directional destination” to the next.

---

David Reinfurt: eveRything is in eveRything

"Everything, every “thing,” takes meaning only by interaction with some- thing else. Indeed its existence cannot be known without such interaction. Both physically and conceptually the qualities of things are discernible only by the response of an external probe interacting with their internal structure. The real units of the world are not particles — atoms, in whatever sense one uses the word—but connections, and a connection must be between two things.

Cyril stanley smith, institute Professor emeritus at Massachusetts institute of technology1 continues in his article, “Dimensionality, valence and Aggregation,” to describe the relationship of these dynamic connections to a “thing.” he says of finding a “thing” in the world, that “it is all a question of what connections are actually established at the time of observation.” if the connections change, the “thing” changes.

and continues: There has been much speculation as to why the world in which we live seems to be three-dimensional. Our experience as children learning by moving and poking and acquiring a sense of inside, outside, flexibility and solidity makes us think of dimensionality in terms of points, polygons and polyhedra, the things so beautifully related by Euler’s Law. I contend that polygons and polyhedra do not exist but only what Arthur Loeb in private conversation has called polyvertices. Polygons and polyhedra mark the negation of connections, and their seeming reality is a mere construct of the human senses responding to gradients of density of vertices with one-dimensional interconnections. Both polygons and polyhedra can be shrunk to points without any change in external connections. Whether or not they appear is entirely a matter of choice, of the scale or resolution of the means of observation.

Whether or not a connection between two vertices is actually made is a question of time — of perhaps more properly the inverse, that time is the sequence of connections. The changing present is a sort of moire ́ pattern formed between the structures of past and future."

http://en.wikipedia.org/wiki/Polygon

https://en.wikipedia.org/wiki/Polyhedron

---

Labanotation