User:Shoebby/Webby Sprouts: Difference between revisions
No edit summary |
|||
| Line 84: | Line 84: | ||
===== The Canvas Element ===== | ===== The Canvas Element ===== | ||
function tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth) { | |||
console.log("entered tree depth: " + depth) | |||
console.log("(" + x1 + ", " + y1 + ") to (" + x2 + ", " + y2 + ")"); | |||
if (depth <= 0) { | |||
return; | |||
} | |||
ctx.strokeStyle = "rgb(" + (parseInt(depth)*10) + " " + (parseInt(depth)*3) + " " + (parseInt(depth)*14) + ")"; | |||
if (depth == 1) { | |||
ctx.fillStyle = "white"; | |||
ctx.strokeStyle = "white"; | |||
ctx.beginPath(); | |||
ctx.arc(x2, y2, 5, 0, Math.PI * 2, false); | |||
ctx.fill(); | |||
} | |||
ctx.moveTo(x1, y1); | |||
ctx.lineTo(x2, y2); | |||
ctx.stroke(); | |||
var base = new Vector2(x2 - x1, y2 - y1); | |||
var new_base = base.clone().multiplyScalar(ratio); | |||
var angleLeft_rad = MathUtils.degToRad(angleLeft); | |||
var angleRight_rad = MathUtils.degToRad(angleRight); | |||
var left = new_base.clone().rotateAround(new Vector2(0, 0), -angleLeft_rad); | |||
var right = new_base.clone().rotateAround(new Vector2(0, 0), angleRight_rad); | |||
var end = new Vector2(x2, y2); | |||
var left_end = end.clone().add(left); | |||
var right_end = end.clone().add(right); | |||
tree(x2, y2, left_end.x, left_end.y, angleLeft, angleRight, ratio, depth - 1); | |||
tree(x2, y2, right_end.x, right_end.y, angleLeft, angleRight, ratio, depth - 1); | |||
} | |||
<gallery mode="packed" widths="300" heights="200"> | <gallery mode="packed" widths="300" heights="200"> | ||
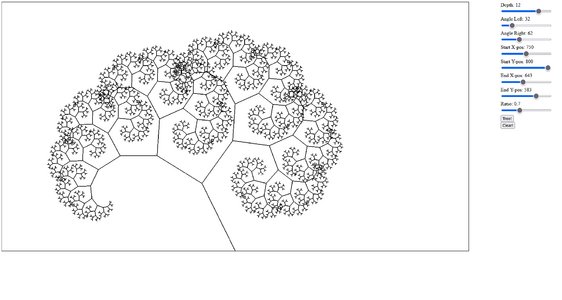
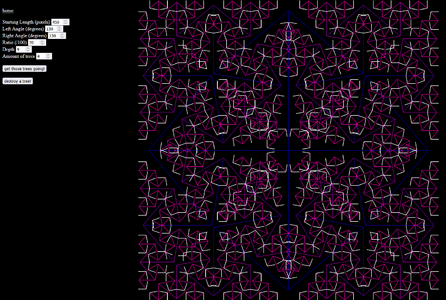
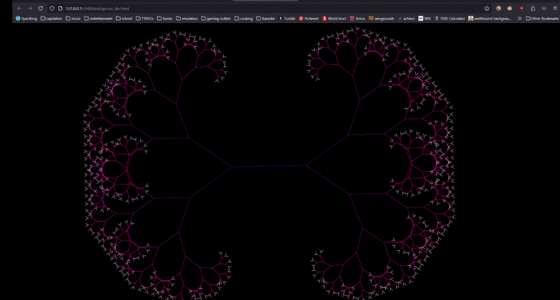
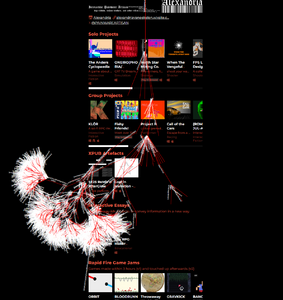
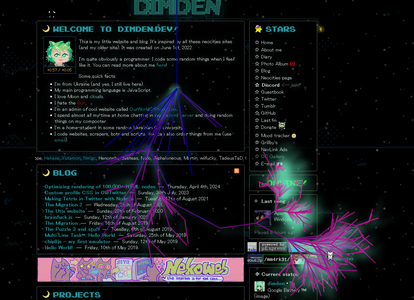
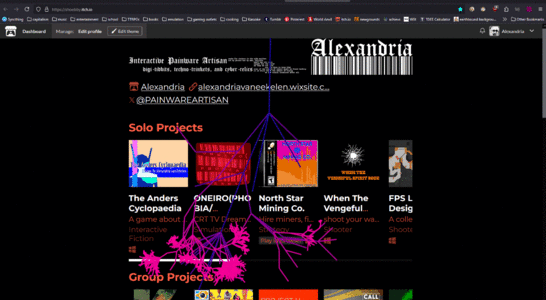
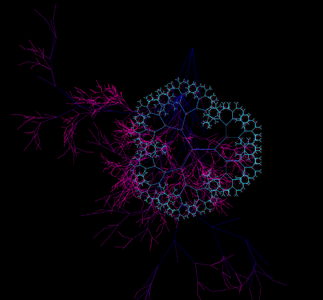
3 canvas 1.png|Now taking fractals fully digital I used the canvas element to generate them, generate your own [https://shoebby.github.io/dist/sprout.html here]! | 3 canvas 1.png|Now taking fractals fully digital I used the canvas element to generate them, generate your own [https://shoebby.github.io/dist/sprout.html here]! | ||
Revision as of 04:21, 31 March 2025
Download here: https://addons.mozilla.org/en-US/firefox/addon/webby-sprouts/
blogpost: https://www.lexie.land/dist/blogpost-penplot.html
(Where am I in) The Process
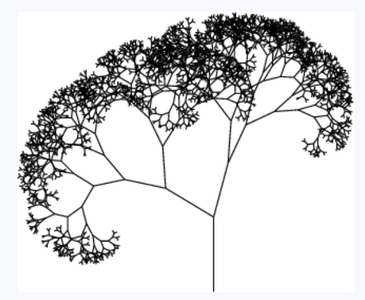
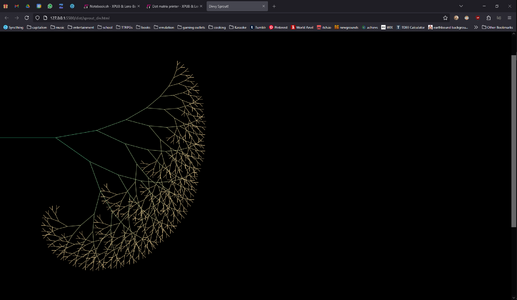
My dive into fractals brought me into contact with a lot of different mediums for drawing them, here is the process shown by way of images in (rough) chronological order.
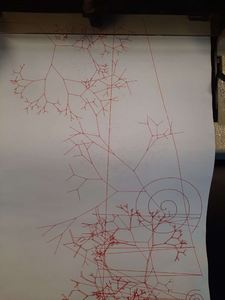
Pen Plotting
import math
import numpy as np
file = open("fractal.hgl", "w")
def rotate(vec, angle):
rads = math.radians(angle)
a = math.cos(rads)
b = math.sin(rads)
R = np.array([[a,-b], [b,a]])
return np.dot(R, vec)
def tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth):
if depth == 0: return
file.write(f'PU {round(x1)},{round(y1)};\n')
file.write(f'PD {round(x2)},{round(y2)};\n')
base = np.array([x2 - x1, y2 - y1])
new_base = base * ratio
right = rotate(new_base, angleRight)
left = rotate(new_base, -angleLeft)
end = np.array([x2, y2])
right_end = np.add(end, right)
left_end = np.add(end, left)
tree(x2, y2, right_end[0], right_end[1], angleLeft, angleRight, ratio, depth - 1)
tree(x2, y2, left_end[0], left_end[1], angleLeft, angleRight, ratio, depth - 1)
print("What's the stem's starting x position? (whole numbers)")
start_x = int(input())
print("What's the stem's starting y position? (whole numbers)")
start_y = int(input())
print("What's the stem's end x position? (whole numbers)")
end_x = int(input())
print("What's the stem's end y position? (whole numbers)")
end_y = int(input())
print("Are the branch angles symmetrical? (y/n)")
symmetrical = input().lower().strip() == "y"
if symmetrical:
print("What angle are the branches? (in degrees, whole numbers)")
angle = int(input())
angleLeft = angle
angleRight = angle
else:
print("What angle is the left branch? (in degrees, whole numbers)")
angleLeft = int(input())
print("What angle is the right branch? (in degrees, whole numbers)")
angleRight = int(input())
print("What ratio should the branches be? (decimal numbers (i.e. .75)) >1 means the branches grow with every recursion, <1 means they shrink.")
ratio = float(input())
print("How many recursions should this fractal be? (whole numbers) 5-10 is usually a good starting point to get an idea of the overall shape.)")
recursions = int(input())
tree(start_x, start_y, end_x, end_y, angleLeft, angleRight, ratio, recursions)
The Canvas Element
function tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth) {
console.log("entered tree depth: " + depth)
console.log("(" + x1 + ", " + y1 + ") to (" + x2 + ", " + y2 + ")");
if (depth <= 0) {
return;
}
ctx.strokeStyle = "rgb(" + (parseInt(depth)*10) + " " + (parseInt(depth)*3) + " " + (parseInt(depth)*14) + ")";
if (depth == 1) {
ctx.fillStyle = "white";
ctx.strokeStyle = "white";
ctx.beginPath();
ctx.arc(x2, y2, 5, 0, Math.PI * 2, false);
ctx.fill();
}
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.stroke();
var base = new Vector2(x2 - x1, y2 - y1);
var new_base = base.clone().multiplyScalar(ratio);
var angleLeft_rad = MathUtils.degToRad(angleLeft);
var angleRight_rad = MathUtils.degToRad(angleRight);
var left = new_base.clone().rotateAround(new Vector2(0, 0), -angleLeft_rad);
var right = new_base.clone().rotateAround(new Vector2(0, 0), angleRight_rad);
var end = new Vector2(x2, y2);
var left_end = end.clone().add(left);
var right_end = end.clone().add(right);
tree(x2, y2, left_end.x, left_end.y, angleLeft, angleRight, ratio, depth - 1);
tree(x2, y2, right_end.x, right_end.y, angleLeft, angleRight, ratio, depth - 1);
}
Now taking fractals fully digital I used the canvas element to generate them, generate your own here!
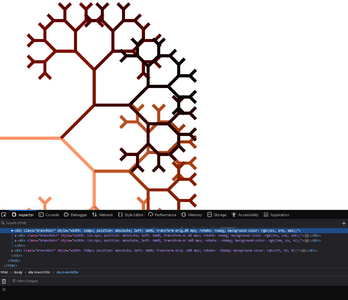
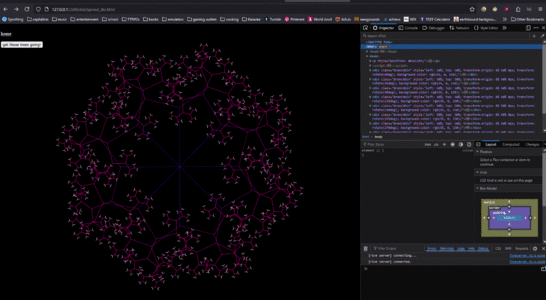
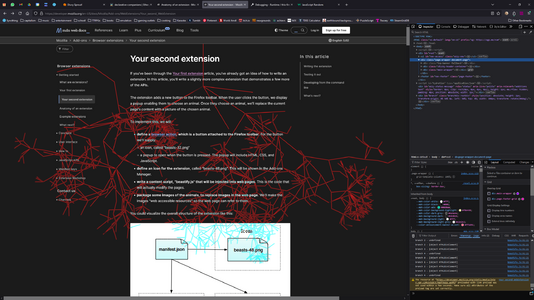
Fractals From Divs
It works, and I could even apply past things like uneven left/right angles already, play with it yourself here