User:Simon/Special Issue 8/summary second half trim: Difference between revisions
No edit summary |
|||
| Line 10: | Line 10: | ||
[http://pzwiki.wdka.nl/mediadesign/User:Simon/Special_Issue_8/knotboard_knots_nodes Knotboard, Knots and Nodes] | [http://pzwiki.wdka.nl/mediadesign/User:Simon/Special_Issue_8/knotboard_knots_nodes Knotboard, Knots and Nodes] | ||
==networked research== | |||
I also began to write down my thoughts on various topics that came up.<br> | |||
[[File:Strips 02.jpg|600px]]<br> | |||
https://pad.xpub.nl/p/networked_research<br> | |||
As I wanted a fairly horizontal structure to my research, I decided to base the content for each page of my website on a walk. | |||
==drawing visualisations== | |||
Drawing (by hand and using vectors) became a large part of the outcomes I produced as part of my research. The drawings often shifted between "hand-drawn" and "computer-drawn", for example, I would use a .svg file made from one of my GPS walks in a vector graphics program, then print it and hand-draw with pencil over the top.<br> | |||
Abstraction became a key interest, and I started to think more about how these different ways of visualising all employed some level of abstraction in order to communicate. This brought me back to the typical idea of displaying network topology, as nodes and straight lines:<br> | |||
<br> | |||
[[File:Star topology wht 640.jpg|300px]] | |||
[[File:Bus wht topology 640.jpg|300px]] | |||
[[File:Ring wht topology 640.jpg|300px]] | |||
[[File:Mesh wht topology 640.jpg|300px]] | |||
<br> | |||
The drawings I made while GPS walking employed straight lines between trackpoints. However, this was just an abstraction - there are no straight lines in reality. In fact, the more accurately I would be able to map the network, the less useful it would be as a readily comprehensible visualisation. I also noticed that at points the GPS signal had become confused or obscured - this happened when I went into buildings (such as a cafe to buy a coffee) or when the signal might have been obscured by tall buildings around me. This produced knots, which I saw as analogous to nodes.<br> | |||
<br> | |||
[[File:Knot scale times four 640.jpg]] | |||
When I imported the lines I made by GPS walking into .svg format, I experimented with unraveling some of these knots, and then drew this process.<br> | |||
<br> | |||
[[File:Unravelled knot 03 640.jpg]] | |||
[[File:Unravelled knot 02 640.jpg]] | |||
[[File:Unravelled knot 01 640.jpg]] | |||
<br> | |||
==knotboard, knots, knotworks== | |||
Early on in my research into network topologies I discovered the klein form, a "non-orientable surface".<br> | |||
[[File:Klein form.jpg|600px]] | |||
<br> | |||
<br> | |||
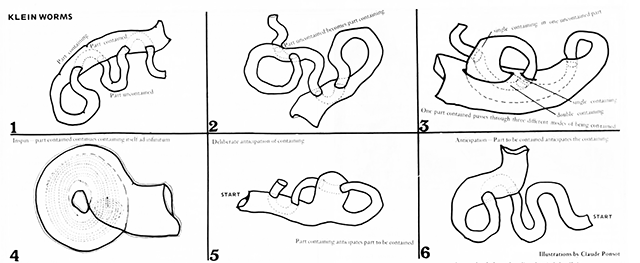
Klein forms are the basis for the "topologically impossible" klein worms. I first came across these in the first half of the trimester as illustrations in the article "Cybernetic Guerilla Warfare" from the media art newsletter '''Radical Software''':<br> | |||
[[File:Hu-02-ponsot-klein-worms-1971.png]]<br> | |||
<br> | |||
<br> | |||
The networked methodology I was working with included shifting between different outcomes and actions. This made me think of also a shift between two-dimensional and three-dimensional forms, and thinking about how these could be "unfolded":<br> | |||
[[File:Mandarin whole.jpg|400px]] | |||
[[File:Mandarin peel 01.jpg|400px]] | |||
[[File:Mandarin peel 02.jpg|400px]] | |||
[[File:Mandarin peel 03.jpg|400px]] | |||
<br> | |||
<br> | |||
The knotboard I had made in the first half of the trimester proved a useful tool for thinking with my hands. I noticed that as a physical object, it was different from my drawings as it immediately had depth, and form, and as a result was affected by light, particularly shadows:<br> | |||
[[File:knot board 09.jpg|400px]] | |||
[[File:knot board 10.jpg|400px]] | |||
[[File:knot board 11.jpg|400px]] | |||
[[File:knot board 12.jpg|400px]] | |||
<br> | |||
<br> | |||
When configured in different ways (especially as a three-dimensional form) the knotboard took on a different presence. I made drawings from this, incorporating light and shadow as well as alternative ways of imagining the three-dimensional space the knotted links occupied:<br> | |||
[[File:Knot board drawing 01 640.jpg]] | |||
[[File:Knot board drawing 02 640.jpg]] | |||
<br> | |||
<br> | |||
Research into knot theory (a field of mathematics which studies the topology of knots) led me to discovering mathematical knots, which are different from the usual idea of a knot. I had previously explored knots as ways to record numbers (a notable reference being Quipu from ancient Andean cultures):<br> | |||
[[File:4 inca quipu knots 640.jpg]]<br> | |||
<br> | |||
Mathematical knots are different, in that they are based on the embedding of a circle into three-dimensional Euclidean geometry R3. As such, they resemble closed loops. The first of these is the "unknot":<br> | |||
[[File:Unknot 640.jpg]]<br> | |||
<br> | |||
Visualisation is a powerful tool when communicating alternative ways of thinking and "seeing" things. Through visualisation, I found another way of thinking about nodes and links. I made "Knotwork" drawings of knots with eight crossings, each representing a node in our homebrewed network. The crossings could be seen as redistribution points (as in the classic definition of a node), or perhaps an overlapping area of linkage. In respect to thinking about nodes as knots, I found that when the knot is unraveled, the nodes and the links are the same thing.<br> | |||
[[File:Knotwork 01 640.jpg|640px]] | |||
[[File:Knotwork 02 640.jpg|640px]] | |||
[[File:Knotwork 03 640.jpg|640px]] | |||
[[File:Knotwork 04 640.jpg|640px]] | |||
[[File:Knotwork 05 640.jpg|640px]] | |||
[[File:Knotwork 07 640.jpg|640px]] | |||
<br> | |||
Revision as of 15:41, 8 April 2019
Visualising network topologies
networked research
I also began to write down my thoughts on various topics that came up.

https://pad.xpub.nl/p/networked_research
As I wanted a fairly horizontal structure to my research, I decided to base the content for each page of my website on a walk.
drawing visualisations
Drawing (by hand and using vectors) became a large part of the outcomes I produced as part of my research. The drawings often shifted between "hand-drawn" and "computer-drawn", for example, I would use a .svg file made from one of my GPS walks in a vector graphics program, then print it and hand-draw with pencil over the top.
Abstraction became a key interest, and I started to think more about how these different ways of visualising all employed some level of abstraction in order to communicate. This brought me back to the typical idea of displaying network topology, as nodes and straight lines:
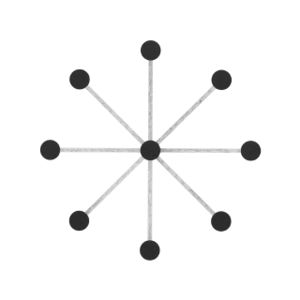
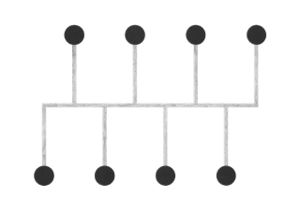
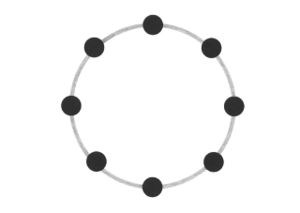
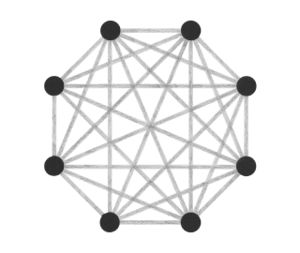
The drawings I made while GPS walking employed straight lines between trackpoints. However, this was just an abstraction - there are no straight lines in reality. In fact, the more accurately I would be able to map the network, the less useful it would be as a readily comprehensible visualisation. I also noticed that at points the GPS signal had become confused or obscured - this happened when I went into buildings (such as a cafe to buy a coffee) or when the signal might have been obscured by tall buildings around me. This produced knots, which I saw as analogous to nodes.
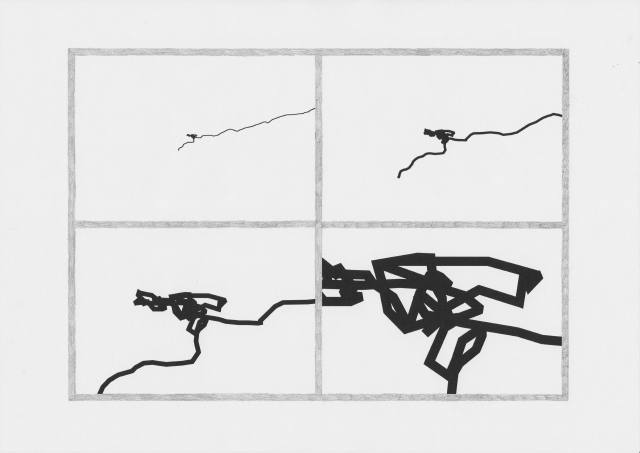
When I imported the lines I made by GPS walking into .svg format, I experimented with unraveling some of these knots, and then drew this process.



knotboard, knots, knotworks
Early on in my research into network topologies I discovered the klein form, a "non-orientable surface".
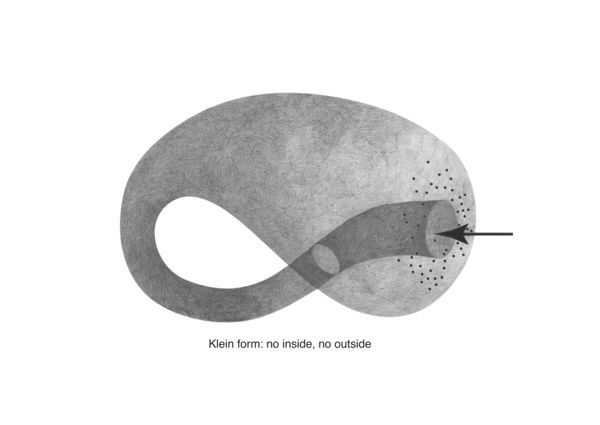
Klein forms are the basis for the "topologically impossible" klein worms. I first came across these in the first half of the trimester as illustrations in the article "Cybernetic Guerilla Warfare" from the media art newsletter Radical Software:
The networked methodology I was working with included shifting between different outcomes and actions. This made me think of also a shift between two-dimensional and three-dimensional forms, and thinking about how these could be "unfolded":




The knotboard I had made in the first half of the trimester proved a useful tool for thinking with my hands. I noticed that as a physical object, it was different from my drawings as it immediately had depth, and form, and as a result was affected by light, particularly shadows:




When configured in different ways (especially as a three-dimensional form) the knotboard took on a different presence. I made drawings from this, incorporating light and shadow as well as alternative ways of imagining the three-dimensional space the knotted links occupied:
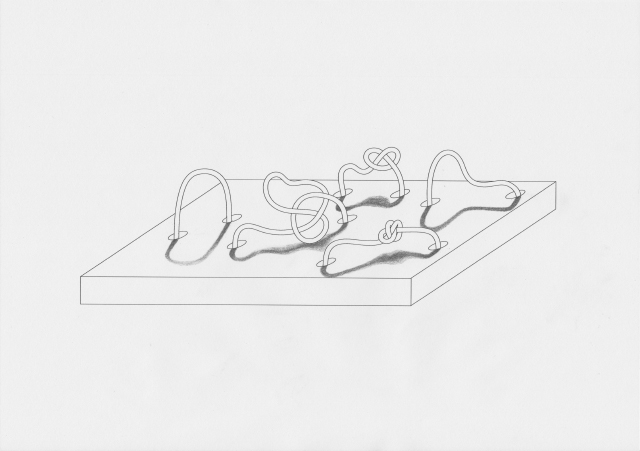

Research into knot theory (a field of mathematics which studies the topology of knots) led me to discovering mathematical knots, which are different from the usual idea of a knot. I had previously explored knots as ways to record numbers (a notable reference being Quipu from ancient Andean cultures):

Mathematical knots are different, in that they are based on the embedding of a circle into three-dimensional Euclidean geometry R3. As such, they resemble closed loops. The first of these is the "unknot":

Visualisation is a powerful tool when communicating alternative ways of thinking and "seeing" things. Through visualisation, I found another way of thinking about nodes and links. I made "Knotwork" drawings of knots with eight crossings, each representing a node in our homebrewed network. The crossings could be seen as redistribution points (as in the classic definition of a node), or perhaps an overlapping area of linkage. In respect to thinking about nodes as knots, I found that when the knot is unraveled, the nodes and the links are the same thing.






