User:Manetta/annotations-of-a-mathemathical-theory-of-communication: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<div style="width:45%;font-size:12pt;"> | <div style="width:45%;font-size:12pt;"> | ||
'''annotations of 'a mathematical theory of communication' ''' | |||
'a mathematical theory of communication' | |||
The word 'communication' includes all procedures by which one mind (or broader: mechanism) affects another. Problems within communication could be divided up in three levels: technical (level A), semantic (level B), and effectiveness (level C) problems. The technical problem seems artificial, and involving only engineering problems, but it affects the other two levels. | The word 'communication' includes all procedures by which one mind (or broader: mechanism) affects another. Problems within communication could be divided up in three levels: technical (level A), semantic (level B), and effectiveness (level C) problems. The technical problem seems artificial, and involving only engineering problems, but it affects the other two levels. | ||
Latest revision as of 12:27, 27 November 2014
annotations of 'a mathematical theory of communication'
The word 'communication' includes all procedures by which one mind (or broader: mechanism) affects another. Problems within communication could be divided up in three levels: technical (level A), semantic (level B), and effectiveness (level C) problems. The technical problem seems artificial, and involving only engineering problems, but it affects the other two levels.
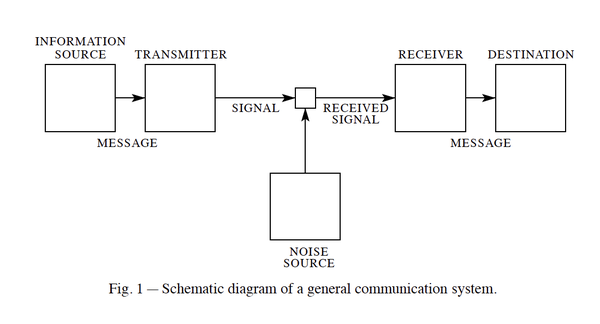
Shannon symbolically represented the communication system into a set of elements (see diagram). Weaver will speak about Shannon's main results that lead to this mathematic terminology, starting with 'information'.
Information must not be confused with meaning, it doesn't relate to what you do say, but to what you could say; information is a measure of one's freedom of choice when one selects a message. One possible message is called an unit of information, which is named a 'bit'. It deals with a two-choise situation (dual). Information is therefor defined through the logarithm (22=4, 23=8) of the number of choises.
As some word or letter combinations are more common than others in the English language, they all have their own probability in the generation of a message. This probability of choise is connected to the concept of 'entropy' in physical science, where the entropy is a variable which measures the degree of 'shuffledness' in a situation, influenced by the contextual factors of energy and temperature.
When a situation is highly organized (not having a large degree of choise), one can say that the information is low. The freedom that the source has in its choise of symbols to form the specific message could be expressed in the degree of relative entropy that applies to the specific situation. The difference between the maximum entropy and the relative entropy is called redundancy. The general English redundancy is 50% (.5).
Information has a statistical nature, and therefore it is able to deal with every kind of intormation. But, when it is not possible to design a system that can handle every message perfectly, it should be designed to be the most effective for a specific source.
In sum: the more freedom of choise there is, the more 'information' the message contains.
(this is only a summary of the first half of the text, which speaks about 'information')