User:Shoebby/Webby Sprouts: Difference between revisions
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Download here: https://addons.mozilla.org/en-US/firefox/addon/webby-sprouts/ | Download here: https://addons.mozilla.org/en-US/firefox/addon/webby-sprouts/ | ||
blogpost: https:// | blogpost: https://www.lexie.land/dist/blogpost-penplot.html | ||
==== (Where am I in) The Process ==== | ==== (Where am I in) The Process ==== | ||
| Line 7: | Line 7: | ||
===== Pen Plotting ===== | ===== Pen Plotting ===== | ||
<gallery mode="packed" widths=300 heights=200> | import math | ||
import numpy as np | |||
file = open("fractal.hgl", "w") | |||
def rotate(vec, angle): | |||
rads = math.radians(angle) | |||
a = math.cos(rads) | |||
b = math.sin(rads) | |||
R = np.array([[a,-b], [b,a]]) | |||
return np.dot(R, vec) | |||
def tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth): | |||
if depth == 0: return | |||
file.write(f'PU {round(x1)},{round(y1)};\n') | |||
file.write(f'PD {round(x2)},{round(y2)};\n') | |||
base = np.array([x2 - x1, y2 - y1]) | |||
new_base = base * ratio | |||
right = rotate(new_base, angleRight) | |||
left = rotate(new_base, -angleLeft) | |||
end = np.array([x2, y2]) | |||
right_end = np.add(end, right) | |||
left_end = np.add(end, left) | |||
tree(x2, y2, right_end[0], right_end[1], angleLeft, angleRight, ratio, depth - 1) | |||
tree(x2, y2, left_end[0], left_end[1], angleLeft, angleRight, ratio, depth - 1) | |||
print("What's the stem's starting x position? (whole numbers)") | |||
start_x = int(input()) | |||
print("What's the stem's starting y position? (whole numbers)") | |||
start_y = int(input()) | |||
print("What's the stem's end x position? (whole numbers)") | |||
end_x = int(input()) | |||
print("What's the stem's end y position? (whole numbers)") | |||
end_y = int(input()) | |||
print("Are the branch angles symmetrical? (y/n)") | |||
symmetrical = input().lower().strip() == "y" | |||
if symmetrical: | |||
print("What angle are the branches? (in degrees, whole numbers)") | |||
angle = int(input()) | |||
angleLeft = angle | |||
angleRight = angle | |||
else: | |||
print("What angle is the left branch? (in degrees, whole numbers)") | |||
angleLeft = int(input()) | |||
print("What angle is the right branch? (in degrees, whole numbers)") | |||
angleRight = int(input()) | |||
print("What ratio should the branches be? (decimal numbers (i.e. .75)) >1 means the branches grow with every recursion, <1 means they shrink.") | |||
ratio = float(input()) | |||
print("How many recursions should this fractal be? (whole numbers) 5-10 is usually a good starting point to get an idea of the overall shape.)") | |||
recursions = int(input()) | |||
tree(start_x, start_y, end_x, end_y, angleLeft, angleRight, ratio, recursions) | |||
<gallery mode="packed" widths="300" heights="200"> | |||
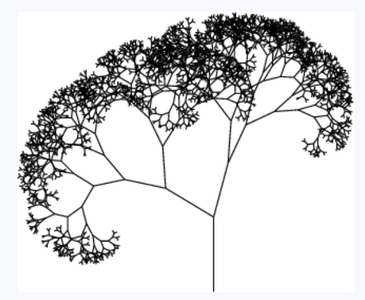
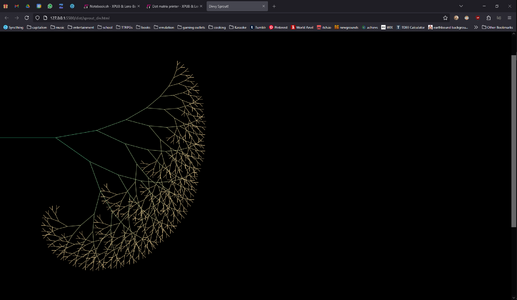
1 penplot 1.jpg|First fractal, made using the pen plotter and a Math'd python script to generate instructions | 1 penplot 1.jpg|First fractal, made using the pen plotter and a Math'd python script to generate instructions | ||
1 penplot 2.mp4|Video of the first fractal being drawn, you can hear my partner in the background 'ooh' and 'aah'ing | 1 penplot 2.mp4|Video of the first fractal being drawn, you can hear my partner in the background 'ooh' and 'aah'ing | ||
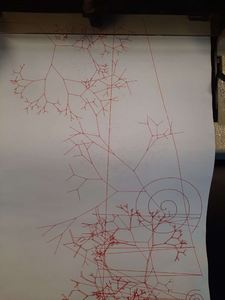
| Line 23: | Line 83: | ||
</gallery> | </gallery> | ||
===== | ===== The Canvas Element ===== | ||
< | function tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth) { | ||
console.log("entered tree depth: " + depth) | |||
console.log("(" + x1 + ", " + y1 + ") to (" + x2 + ", " + y2 + ")"); | |||
if (depth <= 0) { | |||
return; | |||
} | |||
ctx.strokeStyle = "rgb(" + (parseInt(depth)*10) + " " + (parseInt(depth)*3) + " " + (parseInt(depth)*14) + ")"; | |||
if (depth == 1) { | |||
ctx.fillStyle = "white"; | |||
ctx.strokeStyle = "white"; | |||
ctx.beginPath(); | |||
ctx.arc(x2, y2, 5, 0, Math.PI * 2, false); | |||
ctx.fill(); | |||
} | |||
ctx.moveTo(x1, y1); | |||
ctx.lineTo(x2, y2); | |||
ctx.stroke(); | |||
var base = new Vector2(x2 - x1, y2 - y1); | |||
var new_base = base.clone().multiplyScalar(ratio); | |||
var angleLeft_rad = MathUtils.degToRad(angleLeft); | |||
var angleRight_rad = MathUtils.degToRad(angleRight); | |||
var left = new_base.clone().rotateAround(new Vector2(0, 0), -angleLeft_rad); | |||
var right = new_base.clone().rotateAround(new Vector2(0, 0), angleRight_rad); | |||
var end = new Vector2(x2, y2); | |||
var left_end = end.clone().add(left); | |||
var right_end = end.clone().add(right); | |||
tree(x2, y2, left_end.x, left_end.y, angleLeft, angleRight, ratio, depth - 1); | |||
tree(x2, y2, right_end.x, right_end.y, angleLeft, angleRight, ratio, depth - 1); | |||
} | |||
<gallery mode="packed" widths="300" heights="200"> | |||
<gallery mode="packed" widths=300 heights=200> | |||
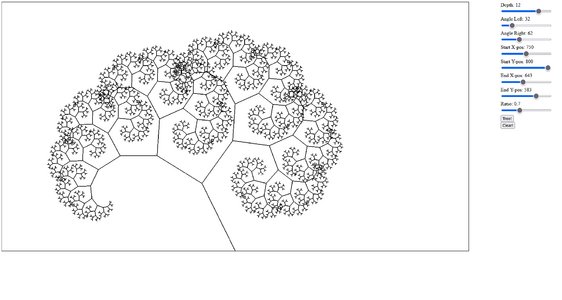
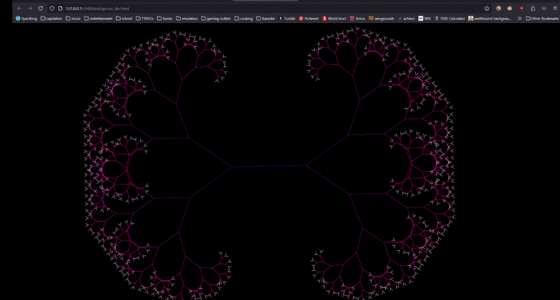
3 canvas 1.png|Now taking fractals fully digital I used the canvas element to generate them, generate your own [https://shoebby.github.io/dist/sprout.html here]! | 3 canvas 1.png|Now taking fractals fully digital I used the canvas element to generate them, generate your own [https://shoebby.github.io/dist/sprout.html here]! | ||
</gallery> | </gallery> | ||
===== Fractals From Divs ===== | ===== Fractals From Divs ===== | ||
<gallery mode="packed" widths=300 heights=200> | function initTrees(treeAmount) { | ||
var startAngle = 360 / treeAmount; | |||
depthstep = 255 / depth; | |||
for (i = 0; i < treeAmount; i++) { | |||
tree(startLength, startAngle*i, depth, null, null, ratio); | |||
} | |||
} | |||
function tree(startLength, startRot, depth, parent, angle, ratio) { | |||
if (depth == 0) { | |||
return; | |||
} | |||
const newBranch = document.createElement("div"); | |||
newBranch.classList.add("branch"); | |||
newBranch.setAttribute("id", "treeBranch"); | |||
if (parent != null) { | |||
parent.appendChild(newBranch); | |||
newBranch.style.setProperty('--w', parent.offsetWidth * ratio + "px"); | |||
newBranch.style.setProperty('--a', angle + "deg"); | |||
} else if (parent == null) { | |||
newBranch.classList.add("root"); | |||
document.body.appendChild(newBranch); | |||
newBranch.style.setProperty('--w', startLength + "px"); | |||
newBranch.style.setProperty('--a', startRot + "deg"); | |||
} | |||
newBranch.innerHTML = "<span>" + newBranch.offsetWidth + "</span>" | |||
newBranch.style.setProperty('--colorR', 255); | |||
newBranch.style.setProperty('--colorG', 255 - (depth * depthstep)); | |||
newBranch.style.setProperty('--colorB', 0); | |||
newBranch.style.setProperty('--colorA', 1); | |||
parent = newBranch; | |||
tree(startLength, startRot, depth - 1, newBranch, angleLeft, ratio); | |||
tree(startLength, startRot, depth - 1, newBranch, -angleRight, ratio); | |||
} | |||
<gallery mode="packed" widths="300" heights="200"> | |||
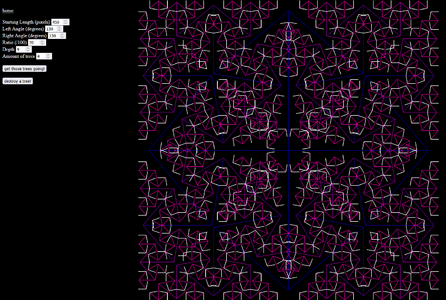
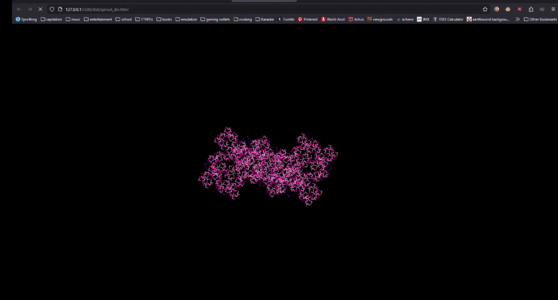
4 divvysprouts 1.png|Canvas didn't really tickle me however, and then Doriane came with the suggestion to instead draw them using divs, which struck me as incredibly cursed and awesome | 4 divvysprouts 1.png|Canvas didn't really tickle me however, and then Doriane came with the suggestion to instead draw them using divs, which struck me as incredibly cursed and awesome | ||
4 divvysprouts 2.png|It works, and I could even apply past things like uneven left/right angles already | 4 divvysprouts 2.png|It works, and I could even apply past things like uneven left/right angles already, play with it yourself [https://shoebby.github.io/dist/sprout_div.html here] | ||
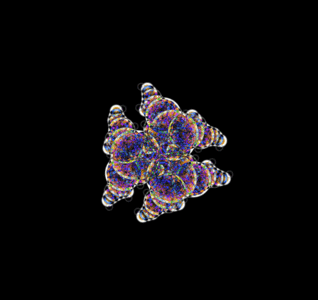
4 divvysprouts 3.png|Squeer | 4 divvysprouts 3.png|Squeer | ||
4 divvysprouts 4.png|Due to the way theyre drawn you can draw multiple over eachother to make neat patterns | 4 divvysprouts 4.png|Due to the way theyre drawn you can draw multiple over eachother to make neat patterns | ||
| Line 54: | Line 189: | ||
===== Fractals From The DOM ===== | ===== Fractals From The DOM ===== | ||
<gallery mode="packed" widths=300 heights=200> | function webTree(startLength, parentElement, parentBranch, angle, ratio, color) { | ||
const newBranch = document.createElement("div"); | |||
newBranch.classList.add("branchDiv"); | |||
parentElement.classList.add("branchElement"); | |||
if (parentBranch != null) { | |||
parentBranch.appendChild(newBranch); | |||
newBranch.style.setProperty('--w', parentBranch.offsetWidth * ratio + "px"); | |||
newBranch.style.setProperty('--a', angle + "deg"); | |||
} else if (parentBranch == null) { | |||
newBranch.classList.add("rootDiv"); | |||
document.body.appendChild(newBranch); | |||
newBranch.style.setProperty('--w', startLength + "px"); | |||
newBranch.style.setProperty('--a', "90deg"); | |||
} | |||
newBranch.style.setProperty('--colorR', 255); | |||
newBranch.style.setProperty('--colorG', 255 - newBranch.offsetWidth); | |||
newBranch.style.setProperty('--colorB', 0); | |||
newBranch.style.setProperty('--colorA', 1); | |||
if (newBranch.hasChildNodes() == false) { | |||
const newBulb = document.createElement("div"); | |||
newBulb.classList.add("branchDiv"); | |||
newBulb.style.height = "50px"; | |||
newBulb.style.width = "50px"; | |||
newBulb.style.backgroundColor = "white"; | |||
} | |||
if (parentElement.tagName == "A") { | |||
newBranch.classList.add('linkFlower'); | |||
newBranch.innerHTML = "<a href=" + parentElement + " style='width:100%;height:100%;'></a>"; | |||
} | |||
var siblings = parentElement.children; | |||
for (let i = 0; i < siblings.length; i++) { | |||
if (siblings[i].classList.contains("branchDiv") || siblings[i].tagName == "BR") { | |||
continue; | |||
} | |||
var newAngle = getRndInteger(-55, 55); | |||
var newRatio = getRndInteger(50, 100) / 100; | |||
webTree(startLength, siblings[i], newBranch, newAngle, newRatio, color); | |||
} | |||
} | |||
<gallery mode="packed" widths="300" heights="200"> | |||
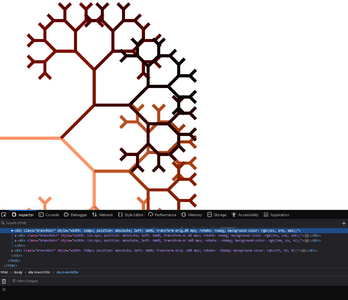
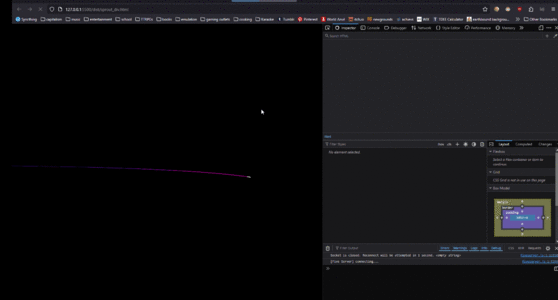
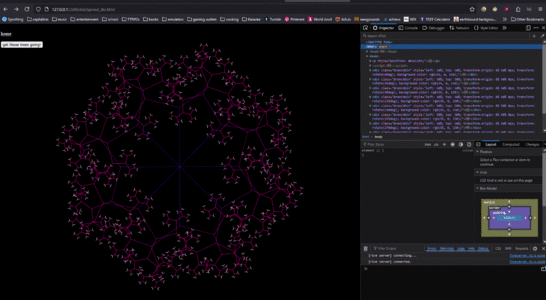
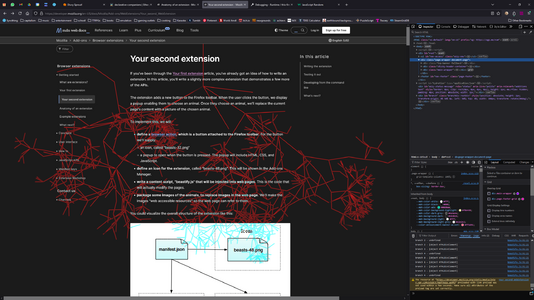
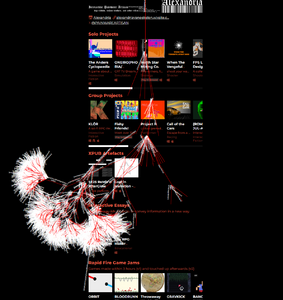
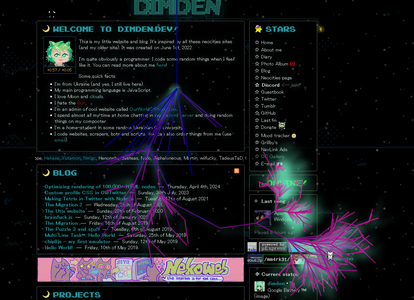
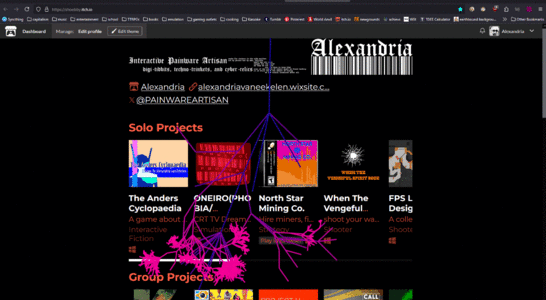
5 webbysprouts 1.png|So now lets take it to a web extension! Assignment: generate a tree fractal based on the webpage DOM | 5 webbysprouts 1.png|So now lets take it to a web extension! Assignment: generate a tree fractal based on the webpage DOM | ||
5 webbysprouts 2.png|And also show what sort of element is related to which branch! | 5 webbysprouts 2.png|And also show what sort of element is related to which branch! | ||
| Line 62: | Line 250: | ||
===== The Final Yuri ===== | ===== The Final Yuri ===== | ||
<gallery mode="packed" widths=300 heights=200> | <gallery mode="packed" widths="300" heights="200"> | ||
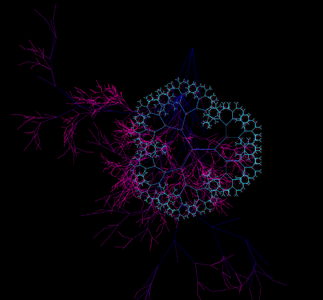
6 finalyuri.png|For fun I also made the divvy sprouts compatible with the webby sprouts, so they could intermingle, pull from eachother, and kiss! | 6 finalyuri.png|For fun I also made the divvy sprouts compatible with the webby sprouts, so they could intermingle, pull from eachother, and kiss! | ||
</gallery> | </gallery> | ||
Revision as of 04:30, 31 March 2025
Download here: https://addons.mozilla.org/en-US/firefox/addon/webby-sprouts/
blogpost: https://www.lexie.land/dist/blogpost-penplot.html
(Where am I in) The Process
My dive into fractals brought me into contact with a lot of different mediums for drawing them, here is the process shown by way of images in (rough) chronological order.
Pen Plotting
import math
import numpy as np
file = open("fractal.hgl", "w")
def rotate(vec, angle):
rads = math.radians(angle)
a = math.cos(rads)
b = math.sin(rads)
R = np.array([[a,-b], [b,a]])
return np.dot(R, vec)
def tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth):
if depth == 0: return
file.write(f'PU {round(x1)},{round(y1)};\n')
file.write(f'PD {round(x2)},{round(y2)};\n')
base = np.array([x2 - x1, y2 - y1])
new_base = base * ratio
right = rotate(new_base, angleRight)
left = rotate(new_base, -angleLeft)
end = np.array([x2, y2])
right_end = np.add(end, right)
left_end = np.add(end, left)
tree(x2, y2, right_end[0], right_end[1], angleLeft, angleRight, ratio, depth - 1)
tree(x2, y2, left_end[0], left_end[1], angleLeft, angleRight, ratio, depth - 1)
print("What's the stem's starting x position? (whole numbers)")
start_x = int(input())
print("What's the stem's starting y position? (whole numbers)")
start_y = int(input())
print("What's the stem's end x position? (whole numbers)")
end_x = int(input())
print("What's the stem's end y position? (whole numbers)")
end_y = int(input())
print("Are the branch angles symmetrical? (y/n)")
symmetrical = input().lower().strip() == "y"
if symmetrical:
print("What angle are the branches? (in degrees, whole numbers)")
angle = int(input())
angleLeft = angle
angleRight = angle
else:
print("What angle is the left branch? (in degrees, whole numbers)")
angleLeft = int(input())
print("What angle is the right branch? (in degrees, whole numbers)")
angleRight = int(input())
print("What ratio should the branches be? (decimal numbers (i.e. .75)) >1 means the branches grow with every recursion, <1 means they shrink.")
ratio = float(input())
print("How many recursions should this fractal be? (whole numbers) 5-10 is usually a good starting point to get an idea of the overall shape.)")
recursions = int(input())
tree(start_x, start_y, end_x, end_y, angleLeft, angleRight, ratio, recursions)
The Canvas Element
function tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth) {
console.log("entered tree depth: " + depth)
console.log("(" + x1 + ", " + y1 + ") to (" + x2 + ", " + y2 + ")");
if (depth <= 0) {
return;
}
ctx.strokeStyle = "rgb(" + (parseInt(depth)*10) + " " + (parseInt(depth)*3) + " " + (parseInt(depth)*14) + ")";
if (depth == 1) {
ctx.fillStyle = "white";
ctx.strokeStyle = "white";
ctx.beginPath();
ctx.arc(x2, y2, 5, 0, Math.PI * 2, false);
ctx.fill();
}
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.stroke();
var base = new Vector2(x2 - x1, y2 - y1);
var new_base = base.clone().multiplyScalar(ratio);
var angleLeft_rad = MathUtils.degToRad(angleLeft);
var angleRight_rad = MathUtils.degToRad(angleRight);
var left = new_base.clone().rotateAround(new Vector2(0, 0), -angleLeft_rad);
var right = new_base.clone().rotateAround(new Vector2(0, 0), angleRight_rad);
var end = new Vector2(x2, y2);
var left_end = end.clone().add(left);
var right_end = end.clone().add(right);
tree(x2, y2, left_end.x, left_end.y, angleLeft, angleRight, ratio, depth - 1);
tree(x2, y2, right_end.x, right_end.y, angleLeft, angleRight, ratio, depth - 1);
}
Now taking fractals fully digital I used the canvas element to generate them, generate your own here!
Fractals From Divs
function initTrees(treeAmount) {
var startAngle = 360 / treeAmount;
depthstep = 255 / depth;
for (i = 0; i < treeAmount; i++) {
tree(startLength, startAngle*i, depth, null, null, ratio);
}
}
function tree(startLength, startRot, depth, parent, angle, ratio) {
if (depth == 0) {
return;
}
const newBranch = document.createElement("div");
newBranch.classList.add("branch");
newBranch.setAttribute("id", "treeBranch");
if (parent != null) {
parent.appendChild(newBranch);
newBranch.style.setProperty('--w', parent.offsetWidth * ratio + "px");
newBranch.style.setProperty('--a', angle + "deg");
} else if (parent == null) {
newBranch.classList.add("root");
document.body.appendChild(newBranch);
newBranch.style.setProperty('--w', startLength + "px");
newBranch.style.setProperty('--a', startRot + "deg");
}
newBranch.innerHTML = "" + newBranch.offsetWidth + ""
newBranch.style.setProperty('--colorR', 255);
newBranch.style.setProperty('--colorG', 255 - (depth * depthstep));
newBranch.style.setProperty('--colorB', 0);
newBranch.style.setProperty('--colorA', 1);
parent = newBranch;
tree(startLength, startRot, depth - 1, newBranch, angleLeft, ratio);
tree(startLength, startRot, depth - 1, newBranch, -angleRight, ratio);
}
It works, and I could even apply past things like uneven left/right angles already, play with it yourself here
Fractals From The DOM
function webTree(startLength, parentElement, parentBranch, angle, ratio, color) {
const newBranch = document.createElement("div");
newBranch.classList.add("branchDiv");
parentElement.classList.add("branchElement");
if (parentBranch != null) {
parentBranch.appendChild(newBranch);
newBranch.style.setProperty('--w', parentBranch.offsetWidth * ratio + "px");
newBranch.style.setProperty('--a', angle + "deg");
} else if (parentBranch == null) {
newBranch.classList.add("rootDiv");
document.body.appendChild(newBranch);
newBranch.style.setProperty('--w', startLength + "px");
newBranch.style.setProperty('--a', "90deg");
}
newBranch.style.setProperty('--colorR', 255);
newBranch.style.setProperty('--colorG', 255 - newBranch.offsetWidth);
newBranch.style.setProperty('--colorB', 0);
newBranch.style.setProperty('--colorA', 1);
if (newBranch.hasChildNodes() == false) {
const newBulb = document.createElement("div");
newBulb.classList.add("branchDiv");
newBulb.style.height = "50px";
newBulb.style.width = "50px";
newBulb.style.backgroundColor = "white";
}
if (parentElement.tagName == "A") {
newBranch.classList.add('linkFlower');
newBranch.innerHTML = "<a href=" + parentElement + " style='width:100%;height:100%;'></a>";
}
var siblings = parentElement.children;
for (let i = 0; i < siblings.length; i++) {
if (siblings[i].classList.contains("branchDiv") || siblings[i].tagName == "BR") {
continue;
}
var newAngle = getRndInteger(-55, 55);
var newRatio = getRndInteger(50, 100) / 100;
webTree(startLength, siblings[i], newBranch, newAngle, newRatio, color);
}
}