User:Shoebby/Webby Sprouts: Difference between revisions
| Line 7: | Line 7: | ||
===== Pen Plotting ===== | ===== Pen Plotting ===== | ||
import math | |||
import numpy as np | |||
file = open("fractal.hgl", "w") | |||
def rotate(vec, angle): | |||
rads = math.radians(angle) | |||
a = math.cos(rads) | |||
b = math.sin(rads) | |||
R = np.array([[a,-b], [b,a]]) | |||
return np.dot(R, vec) | |||
def tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth): | |||
if depth == 0: return | |||
file.write(f'PU {round(x1)},{round(y1)};\n') | |||
file.write(f'PD {round(x2)},{round(y2)};\n') | |||
base = np.array([x2 - x1, y2 - y1]) | |||
new_base = base * ratio | |||
right = rotate(new_base, angleRight) | |||
left = rotate(new_base, -angleLeft) | |||
end = np.array([x2, y2]) | |||
right_end = np.add(end, right) | |||
left_end = np.add(end, left) | |||
tree(x2, y2, right_end[0], right_end[1], angleLeft, angleRight, ratio, depth - 1) | |||
tree(x2, y2, left_end[0], left_end[1], angleLeft, angleRight, ratio, depth - 1) | |||
print("What's the stem's starting x position? (whole numbers)") | |||
start_x = int(input()) | |||
print("What's the stem's starting y position? (whole numbers)") | |||
start_y = int(input()) | |||
print("What's the stem's end x position? (whole numbers)") | |||
end_x = int(input()) | |||
print("What's the stem's end y position? (whole numbers)") | |||
end_y = int(input()) | |||
print("Are the branch angles symmetrical? (y/n)") | |||
symmetrical = input().lower().strip() == "y" | |||
if symmetrical: | |||
print("What angle are the branches? (in degrees, whole numbers)") | |||
angle = int(input()) | |||
angleLeft = angle | |||
angleRight = angle | |||
else: | |||
print("What angle is the left branch? (in degrees, whole numbers)") | |||
angleLeft = int(input()) | |||
print("What angle is the right branch? (in degrees, whole numbers)") | |||
angleRight = int(input()) | |||
print("What ratio should the branches be? (decimal numbers (i.e. .75)) >1 means the branches grow with every recursion, <1 means they shrink.") | |||
ratio = float(input()) | |||
print("How many recursions should this fractal be? (whole numbers) 5-10 is usually a good starting point to get an idea of the overall shape.)") | |||
recursions = int(input()) | |||
tree(start_x, start_y, end_x, end_y, angleLeft, angleRight, ratio, recursions) | |||
<gallery mode="packed" widths="300" heights="200"> | <gallery mode="packed" widths="300" heights="200"> | ||
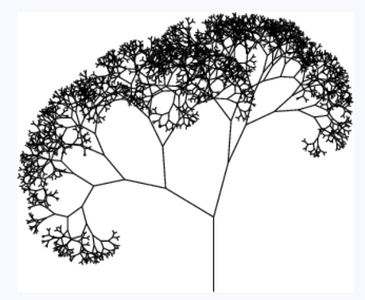
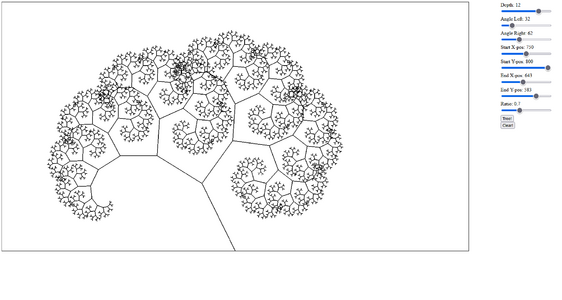
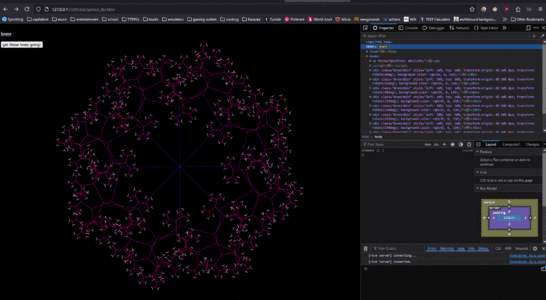
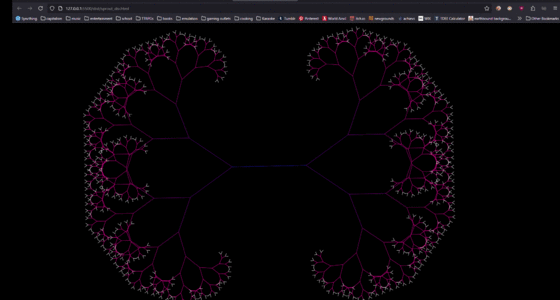
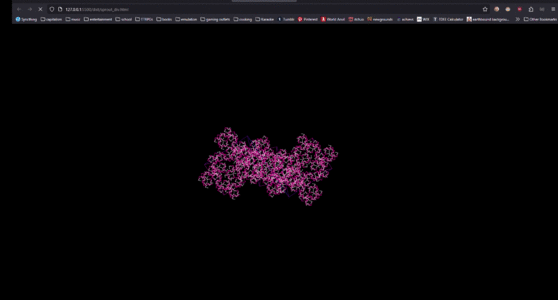
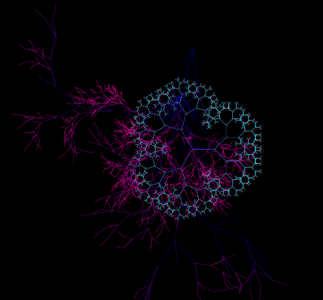
1 penplot 1.jpg|First fractal, made using the pen plotter and a Math'd python script to generate instructions | 1 penplot 1.jpg|First fractal, made using the pen plotter and a Math'd python script to generate instructions | ||
Revision as of 04:16, 31 March 2025
Download here: https://addons.mozilla.org/en-US/firefox/addon/webby-sprouts/
blogpost: https://www.lexie.land/dist/blogpost-penplot.html
(Where am I in) The Process
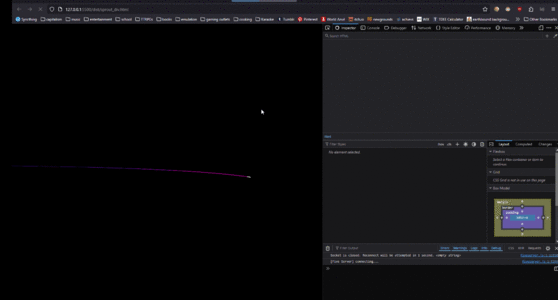
My dive into fractals brought me into contact with a lot of different mediums for drawing them, here is the process shown by way of images in (rough) chronological order.
Pen Plotting
import math
import numpy as np
file = open("fractal.hgl", "w")
def rotate(vec, angle):
rads = math.radians(angle)
a = math.cos(rads)
b = math.sin(rads)
R = np.array([[a,-b], [b,a]])
return np.dot(R, vec)
def tree(x1, y1, x2, y2, angleLeft, angleRight, ratio, depth):
if depth == 0: return
file.write(f'PU {round(x1)},{round(y1)};\n')
file.write(f'PD {round(x2)},{round(y2)};\n')
base = np.array([x2 - x1, y2 - y1])
new_base = base * ratio
right = rotate(new_base, angleRight)
left = rotate(new_base, -angleLeft)
end = np.array([x2, y2])
right_end = np.add(end, right)
left_end = np.add(end, left)
tree(x2, y2, right_end[0], right_end[1], angleLeft, angleRight, ratio, depth - 1)
tree(x2, y2, left_end[0], left_end[1], angleLeft, angleRight, ratio, depth - 1)
print("What's the stem's starting x position? (whole numbers)")
start_x = int(input())
print("What's the stem's starting y position? (whole numbers)")
start_y = int(input())
print("What's the stem's end x position? (whole numbers)")
end_x = int(input())
print("What's the stem's end y position? (whole numbers)")
end_y = int(input())
print("Are the branch angles symmetrical? (y/n)")
symmetrical = input().lower().strip() == "y"
if symmetrical:
print("What angle are the branches? (in degrees, whole numbers)")
angle = int(input())
angleLeft = angle
angleRight = angle
else:
print("What angle is the left branch? (in degrees, whole numbers)")
angleLeft = int(input())
print("What angle is the right branch? (in degrees, whole numbers)")
angleRight = int(input())
print("What ratio should the branches be? (decimal numbers (i.e. .75)) >1 means the branches grow with every recursion, <1 means they shrink.")
ratio = float(input())
print("How many recursions should this fractal be? (whole numbers) 5-10 is usually a good starting point to get an idea of the overall shape.)")
recursions = int(input())
tree(start_x, start_y, end_x, end_y, angleLeft, angleRight, ratio, recursions)
PostScript
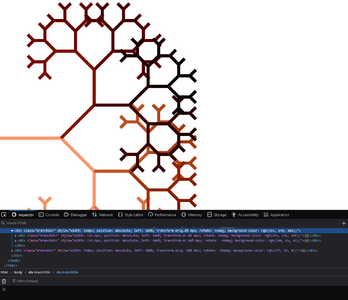
The Canvas Element
Now taking fractals fully digital I used the canvas element to generate them, generate your own here!
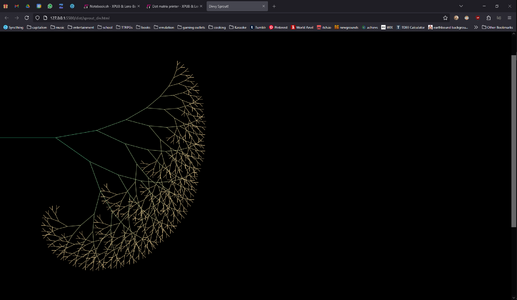
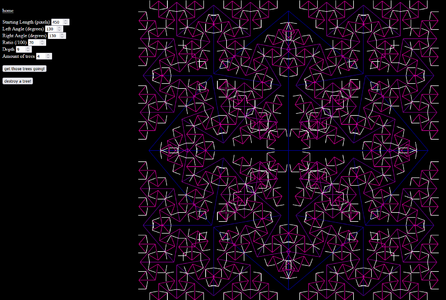
Fractals From Divs
It works, and I could even apply past things like uneven left/right angles already, play with it yourself here