User:Thijshijsijsjss/Pen Plotting Panache/Plotillism: Difference between revisions
(Add photo of moonpool plot) |
(Add details to actual technique used) |
||
| Line 16: | Line 16: | ||
=Technique= | =Technique= | ||
This plotillism software is based on [https://www.cs.ubc.ca/labs/imager/tr/2002/secord2002b/secord.2002b.pdf the 2002 paper by Secord]. This paper suggests the following strategy: | |||
# Randomly place N seed points on your canvas | # Randomly place N seed points on your canvas. There are many ways to do this. | ||
# Create the [https://en.wikipedia.org/wiki/Delaunay_triangulation Delaunay diagram] for these seed points: the unique triangulation such that the no triangles circumcircle contains any points) | # Create the [https://en.wikipedia.org/wiki/Delaunay_triangulation Delaunay diagram] for these seed points: the unique triangulation such that the no triangles circumcircle contains any points) | ||
# Create the [https://en.wikipedia.org/wiki/Voronoi_diagram Voronoi diagram] for these seed points: polygons that represent the areas that contain all coordinates that share the seed point they're closest to. This is the [https://en.wikipedia.org/wiki/Dual_graph dual graph] of the Delaunay diagram (i.e. the vertices in the Voronoi diagram are the centers of the Delaunay circumcircles). | # Create the [https://en.wikipedia.org/wiki/Voronoi_diagram Voronoi diagram] for these seed points: polygons that represent the areas that contain all coordinates that share the seed point they're closest to. This is the [https://en.wikipedia.org/wiki/Dual_graph dual graph] of the Delaunay diagram (i.e. the vertices in the Voronoi diagram are the centers of the Delaunay circumcircles). | ||
# Apply [https://en.wikipedia.org/wiki/Lloyd%27s_algorithm Lloyd's Algorithm (Voronoi iteration)] by iteratively moving the seed points to the centers of the Voronoi polygons. This can be approximated by the average of the polygon vertices, or better yet be calculated ([https://paulbourke.net/geometry/polygonmesh/ see Paul Burke's reference]). | # Apply [https://en.wikipedia.org/wiki/Lloyd%27s_algorithm Lloyd's Algorithm (Voronoi iteration)] by iteratively moving the seed points to the centers of the Voronoi polygons*. This can be approximated by the average of the polygon vertices, or better yet be calculated ([https://paulbourke.net/geometry/polygonmesh/ see Paul Burke's reference]). | ||
# Use these relaxed points for 'pointillism' | # Use these relaxed points for 'pointillism' | ||
Note: for our purposes, we don't simply want to relax all points. This would ultimately lead to a uniform distribution. Instead, we want to base the relaxation on the brightness values of the image we feed in. | '''*Note''': for our purposes, we don't simply want to relax all points. This would ultimately lead to a uniform distribution. Instead, we want to base the relaxation on the brightness values of the image we feed in. The software uses this approach: | ||
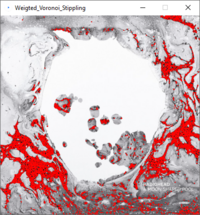
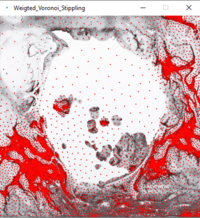
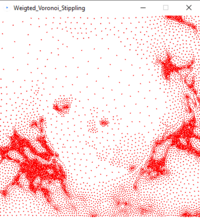
# Randomly place N seed points on your canvas stochastically: choose a random location <code>x,y</code>, produce a random number <code>R</code> between 0 and <code>thresh</code>, and place a point there if and only if <code>R > brightness(x,y)</code>. This stochastic approach produces quite 'good' initial positions, i.e. the points are relatively close to their brightness-weighted equilibrium position (first image). '''O(N) complexity'''. | |||
# Create 'reversed' Voronoi diagrams by looping over all pixels, and assign the closest seed point to it. Note that we have skipped the Delaunay triangulation. Working with polygons is difficult. '''O(W*H*N) complexity'''. | |||
# Relax the seedpoints based on brightness: for every seedpoint, fetch the pixels assigned to it and calculate their weighted centroid as the new seedpoint position. '''O(N*W*H) complexity'''. | |||
=References= | =References= | ||
Revision as of 22:17, 24 May 2024
Stippling is a drawing technique by which details are captured by placing points in varying densities and is frequently used in the impressionistic pointillism. This page describes a workflow to convert a digital image to a pointillism version that can be pen plotted.
- Find the code on GitHub
Technique
This plotillism software is based on the 2002 paper by Secord. This paper suggests the following strategy:
- Randomly place N seed points on your canvas. There are many ways to do this.
- Create the Delaunay diagram for these seed points: the unique triangulation such that the no triangles circumcircle contains any points)
- Create the Voronoi diagram for these seed points: polygons that represent the areas that contain all coordinates that share the seed point they're closest to. This is the dual graph of the Delaunay diagram (i.e. the vertices in the Voronoi diagram are the centers of the Delaunay circumcircles).
- Apply Lloyd's Algorithm (Voronoi iteration) by iteratively moving the seed points to the centers of the Voronoi polygons*. This can be approximated by the average of the polygon vertices, or better yet be calculated (see Paul Burke's reference).
- Use these relaxed points for 'pointillism'
*Note: for our purposes, we don't simply want to relax all points. This would ultimately lead to a uniform distribution. Instead, we want to base the relaxation on the brightness values of the image we feed in. The software uses this approach:
- Randomly place N seed points on your canvas stochastically: choose a random location
x,y, produce a random numberRbetween 0 andthresh, and place a point there if and only ifR > brightness(x,y). This stochastic approach produces quite 'good' initial positions, i.e. the points are relatively close to their brightness-weighted equilibrium position (first image). O(N) complexity. - Create 'reversed' Voronoi diagrams by looping over all pixels, and assign the closest seed point to it. Note that we have skipped the Delaunay triangulation. Working with polygons is difficult. O(W*H*N) complexity.
- Relax the seedpoints based on brightness: for every seedpoint, fetch the pixels assigned to it and calculate their weighted centroid as the new seedpoint position. O(N*W*H) complexity.
References
- Paper introducing Weighted Voronoi Stippling
- Coding Train tutorial and reference code (p5.js using D3 library)
- Wikipedia: Voronoi diagram (basis for relaxation)
- Wikipedia: Delaunay triangulation (dual graph to Voronoi diagram that might be used for optimized pixel-coloring)
- Lloyd's Algorithm (Voronoi iteration) (way of iterative relaxation of seed points)
- Calculating the center of a polygon Paul Burke's reference (not used, this script is using pixel information)