User:Gersande: Difference between revisions

From XPUB & Lens-Based wiki
Line 100: Line 100:
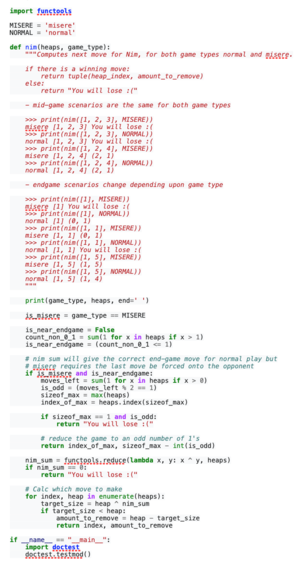
===In Python===
===In Python===


import functools
[[File:Screenshot 2022-02-08 at 15.04.59.png|frameless]]
 
MISERE = 'misere'
NORMAL = 'normal'
 
def nim(heaps, game_type):
    """Computes next move for Nim, for both game types normal and misere.
 
    if there is a winning move:
        return tuple(heap_index, amount_to_remove)
    else:
        return "You will lose :("
 
    - mid-game scenarios are the same for both game types
 
    >>> print(nim([1, 2, 3], MISERE))
    misere [1, 2, 3] You will lose :(
    >>> print(nim([1, 2, 3], NORMAL))
    normal [1, 2, 3] You will lose :(
    >>> print(nim([1, 2, 4], MISERE))
    misere [1, 2, 4] (2, 1)
    >>> print(nim([1, 2, 4], NORMAL))
    normal [1, 2, 4] (2, 1)
 
    - endgame scenarios change depending upon game type
 
    >>> print(nim([1], MISERE))
    misere [1] You will lose :(
    >>> print(nim([1], NORMAL))
    normal [1] (0, 1)
    >>> print(nim([1, 1], MISERE))
    misere [1, 1] (0, 1)
    >>> print(nim([1, 1], NORMAL))
    normal [1, 1] You will lose :(
    >>> print(nim([1, 5], MISERE))
    misere [1, 5] (1, 5)
    >>> print(nim([1, 5], NORMAL))
    normal [1, 5] (1, 4)
    """
 
    print(game_type, heaps, end=' ')
 
    is_misere = game_type == MISERE
 
    is_near_endgame = False
    count_non_0_1 = sum(1 for x in heaps if x > 1)
    is_near_endgame = (count_non_0_1 <= 1)
 
    # nim sum will give the correct end-game move for normal play but
    # misere requires the last move be forced onto the opponent
    if is_misere and is_near_endgame:
        moves_left = sum(1 for x in heaps if x > 0)
        is_odd = (moves_left % 2 == 1)
        sizeof_max = max(heaps)
        index_of_max = heaps.index(sizeof_max)
 
        if sizeof_max == 1 and is_odd:
            return "You will lose :("
 
        # reduce the game to an odd number of 1's
        return index_of_max, sizeof_max - int(is_odd)
 
    nim_sum = functools.reduce(lambda x, y: x ^ y, heaps)
    if nim_sum == 0:
        return "You will lose :("
 
    # Calc which move to make
    for index, heap in enumerate(heaps):
        target_size = heap ^ nim_sum
        if target_size < heap:
            amount_to_remove = heap - target_size
            return index, amount_to_remove
 
if __name__ == "__main__":
    import doctest
    doctest.testmod()


==About Modding==
==About Modding==

Revision as of 15:05, 8 February 2022

Special Issue 16

Online publication

Etc Research

Project Description

The Etc Portal to Contamination is a project initiated by Chaeyoung Kim and Gersande Schellinx in the context of the Special Issue 16 (2021) of the XPUB around the topic of Vernacular Language Processing. It is a subgroup project hosted by the overall project: Learning How To Walk While Catwalking. The three-steps experience offered to the user unfolds as follows: the users enter the "etc-portal", on the other side of that portal is presented to them a text in which "gates"(submit boxes, see image below), each target-word will open a gate to a negative space in the text, created after our text has been processed. Where the space opens up, the users are invited to "contaminate" the text with their own contaminants (ideas, thoughts, anecdotes quotes or other textual matters).

When done with their "contamination", the users are then invited to submit it and shift/rewrite the context of the text. Finally, the text is immediately returned to them with their latest additions.

Collaboration and project archive with Chaeyoung Kim: https://pzwiki.wdka.nl/mediadesign/Etc_Filter_/_Negative_Space_/_Starting_Point

Special Issue 17

Glossary: https://pzwiki.wdka.nl/mediadesign/Glossary_of_productive_play

Visual References

Black Sheep Boy

Balck Sheep Boy 2019.png

https://www.youtube.com/watch?v=riHl1WYfXrU

Puzzles

Nim

Nim 2.png
https://www.youtube.com/watch?v=82l8FtL6Og4
Last Year at Marienbad (L'année dernière à Marienbad by Alain Resnais, 1961)

What is it?

A strategic and mathematical game. Much like Chess and Go, the players need to plan their moves ahead in order to “win” the game. 

                                 _________                                  
                                (  _____  )                                 
                                | |_____| |                                 
                                (_________)    
                            
                      _________  _________  _________                       
                     (  _____  )(  _____  )(  _____  )                      
                     | |_____| || |_____| || |_____| |                      
                     (_________)(_________)(_________)     
                
           _________  _________  _________  _________  _________            
          (  _____  )(  _____  )(  _____  )(  _____  )(  _____  )           
          | |_____| || |_____| || |_____| || |_____| || |_____| |           
          (_________)(_________)(_________)(_________)(_________)    
      
_________  _________  _________  _________  _________  _________  _________

( _____ )( _____ )( _____ )( _____ )( _____ )( _____ )( _____ ) | |_____| || |_____| || |_____| || |_____| || |_____| || |_____| || |_____| | (_________)(_________)(_________)(_________)(_________)(_________)(_________)


The classic game of Nim can have different structures, always composed of a few “heaps” or “rows” of items, any items. The amount can be of 2, 3 or 4 heaps. The one above is 4 heaps: 1, 3, 5 and 7. A peculiarity of the Nim game is that, even if can be played in a normal setting (the player that picks-up the last item wins) it is mostly played as a Misère game, meaning one has to lose the last item to its opponent in order to win. 

        O				O 	                         O
       OOX		               OOX 		                OOO
      OOOOX                          OOOOO 	                       OOOOX
     OOOOOOO    (1, 2, 4, 7)        OOOOOOX. (1, 2, 5, 6)            OOOOOOX. (1, 3, 4, 6)

BEWARE: this game is inherently unfair! Unlike other games there is nothing left to chance. The Nim game is intrinsically an unfair game, as depending of the amount of items in each heaps, one can be sure to win or sure to loose. Also if a player knows the safe positions depending of the amount of pieces in front of him, one can be sure to always be in a winning position (some of the allegedly winning combinations below for the 4 heaps version).

What are the rules?

The rules of the Nim game are quite simple. It is a two players’ game, each player plays one after the other. One can remove as many items as they want each turn, and needs to remove at least one item, as long as they remain in the same row. The next turn they may remove again as many items as they want in another row, as long as it remains in that same row. The last player to pick up an item loses.

What do you need to play this game?

No physical skills require. You need an adversary and 16 pieces of anything. This game can be done on paper, physically, with placards, glasses, peanuts, cigarette butts, coins. As long as you have 4 rows of 1, 3, 5 and 7 items layed out in front of you, you can be “nimming” your adversary away.

What is a Misère game?

A misère game is a game in which the rules which in a “normal” game would bring one to win actually get one to loose. As such the players have to trick their adversary into a “poor” game, it is thus necessary to spare tricks, in order not to acquire but dismiss. The one who looses territory, gains authority.

Ideologies behind the Nim?

Unlike other strategic games such as Go, Chess or even Ought Crosses, the Nim game is very brief and experienced players can already tell after a few turns which player is gonna win or lose the ongoing game, as its mathematical sequence are very dominant visually and tactically. Also, when in Go and Chess, or other similar boardgames the player is overtaking the territorial space of the game in order to corner its opponent and take over its pawns, the take-over in the Nim game is nowhere to be seen but in the players’ mind. In its own way, the Nim “game” is a counter-game as the players are in certain ways with very little to no agency. One player is always ahead of the other, and there are no chance in turning back the table while playing. The win is reversed, one has to escape the urge of dominating the space in order to trick its opponent into the light, at the moment the one losing is in the spotlight, the game has already been lost. In a way the Nim game illustrated all the micro-actions taken by player in order to win in any other more lengthy tactical games, the difference being that while in other games, a player might be overpowered at any moment, in the Nim game, this power dynamic is set in stone quite quickly.

This game fascinates a lot due to its solvable feature, if one has cracked the code, one will always win (or loose rather…), undoubtedly! In a way it is a puzzle to solve with two people but where only one gain from it, and you need that human factor in order to solve the puzzle. The Nim game, formula has been studied, solved, programmed as well by thinkers, mathematicians, programmers and puzzle amateurs. Accessible to any person, of any age or background. It can be seen as a party trick as show-off, but contains some kind of magic for the unexperienced player.

It is said to originate from China, but the sources are uncertain. People would allegedly play on the streets with any kind of junk that could be found around them. Therefore, the Nim game is absolutely not site-specific and can be played anywhere with anything as long as there are two players. Of course one can play alone, but then one doesn’t gain any kind of puzzling satisfaction.

Different Nim games format

DrNimDirections.jpg
> Dr. Nim was a plastic toy invented by John Thomas Godfrey and published by ESR Inc. in 1966. It was the first mass-market consumer product explicitly marketed as a “computer game,”

ONLINE NIM HERE

ANDROID NIM

See Nimbers, Surreal Number

In Python

Screenshot 2022-02-08 at 15.04.59.png

About Modding

Follower of Jheronimus Bosch Christ in Limbo.jpg Warhammer.jpg Wow.jpg

Bilbiography

(i) The Routledge Companion to Video Game Studies edited by Mark J. P. Wolf and Bernard Perron, Chapter 26
(ii) The Player’s Power to Change the Game, Annemarie, Chapter 2
(iii) Predatory monetization schemes in video games (e.g. ‘loot boxes’) and internet gaming disorder, DANIEL L. KING & PAUL H. DELFABBRO
(iv) BASE AND SUPERSTRUCTURE IN MARXIST CULTURAL THEORY, RAYMOND WILLIAMS
(v) Gamification as twenty-first-century ideology, Mathias Fuchs
(vi) Cultural Resistance Reader, Stephen Duncombe, STUART HALL, "NOTES ON DECONSTRUCTING 'THE POPULAR"'
(vii) The Ruling Class and the Ruling Ideas, Marx & Engels
(viii) Steve Bannon Saw the ‘Monster Power’ of Angry Gamers While Farming Gold in World of Warcraft, By Jake Swearingen

Retrieved from "https://pzwiki.wdka.nl/mw-mediadesign/index.php?title=User:Gersande&oldid=209311"