Finite State Machines
Finite state machines add the idea of time to basic logic. Instead of having single "black box" with a single set of inputs and outputs, a finite state machine is like having many boxes, each for a different situation, and where one box is "active" at a time. Then, we use the logic of each box or "state" to determine not only outputs (say, lights or sounds), but also what the "next state" of the machine is. In this way, you can visualize a finite state machine as a kind of graph with nodes that represent the states and transitions between the nodes labelled by the situations that determine when the transitions should occur. In addition to the physical / logical configuration of the states, these signals or transitions would be determined by the inputs coming into that state.
Finite state machines can be thought of as a kind of "Snakes & Ladders game". In this children's board game, a player tries to climb the spaces of a playing board to be the first to reach the top. The player marks his or her position on the board with a token. The player rolls a die and moves his or her token that many spaces on the board. Some squares are linked with ladders, and others with snakes. If a player happens to end up on such a marked square, he or she has the advantage, or misfortune, to have to move their token either up to a later or down to an earlier square on the board.

In this case, each space on the board represents a "state" of the machine. The current state is indicated by the position of the player's token. The "input" to the state is the result of the roll of a die (1 - 6). Slides and ladders are additional transitions between the states (based on no input, or you could say the "input" of a player landing on that square). Thus with this relatively simple structure, the limited inputs (the six sides of the die) produce a variety of results in the game as it depends each time on the current "state" of the game (where the player is at the time the roll of the die occurs).
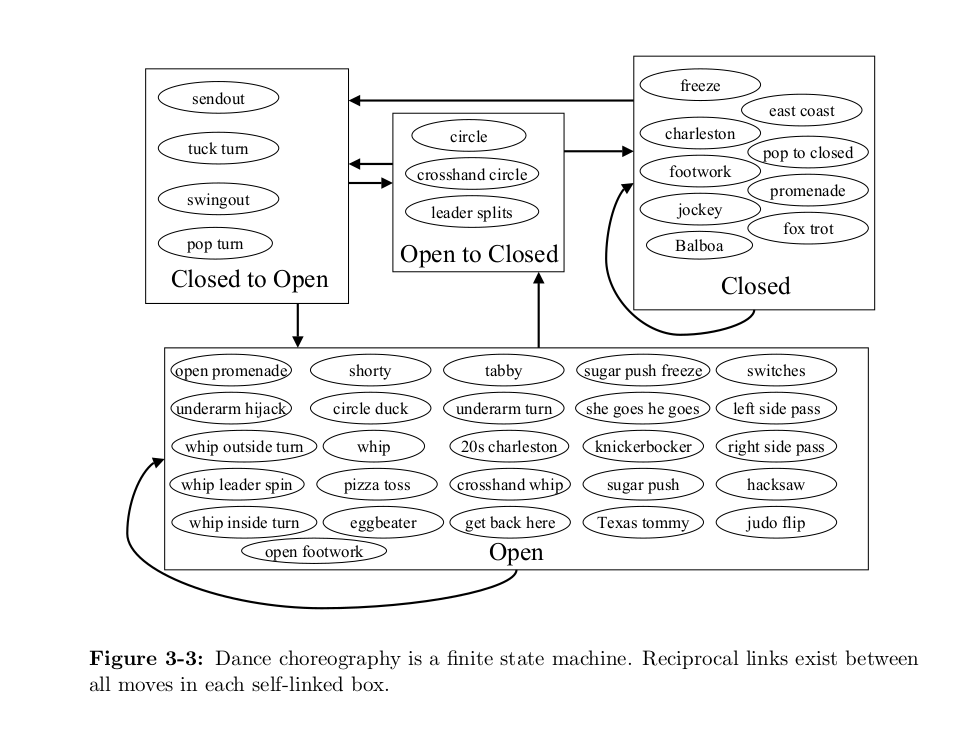
In her 1995 MIT PhD thesis, Sommer Elizabeth Gentry wrote about dancing as a finite state machine.
Another example of a FSM, and one featured in Hillis's Pattern on the Stone, is a traffic light or a combination lock.
Another example might be a telephone system / answering machine.
Next: